分支预测

发表于 2018-08-20 |

GCC 扩展 __builtin_expect

C 语言的标准从最开始的 K&R C演变到目前的 ANSI C，在各操作系统平台已经有很多编译器支持了，如 MSVC、GCC、CLANG 等。而 linux 平台的 GCC 除了支持ANSI C 标准之外，还有自己的编译器扩展特性。

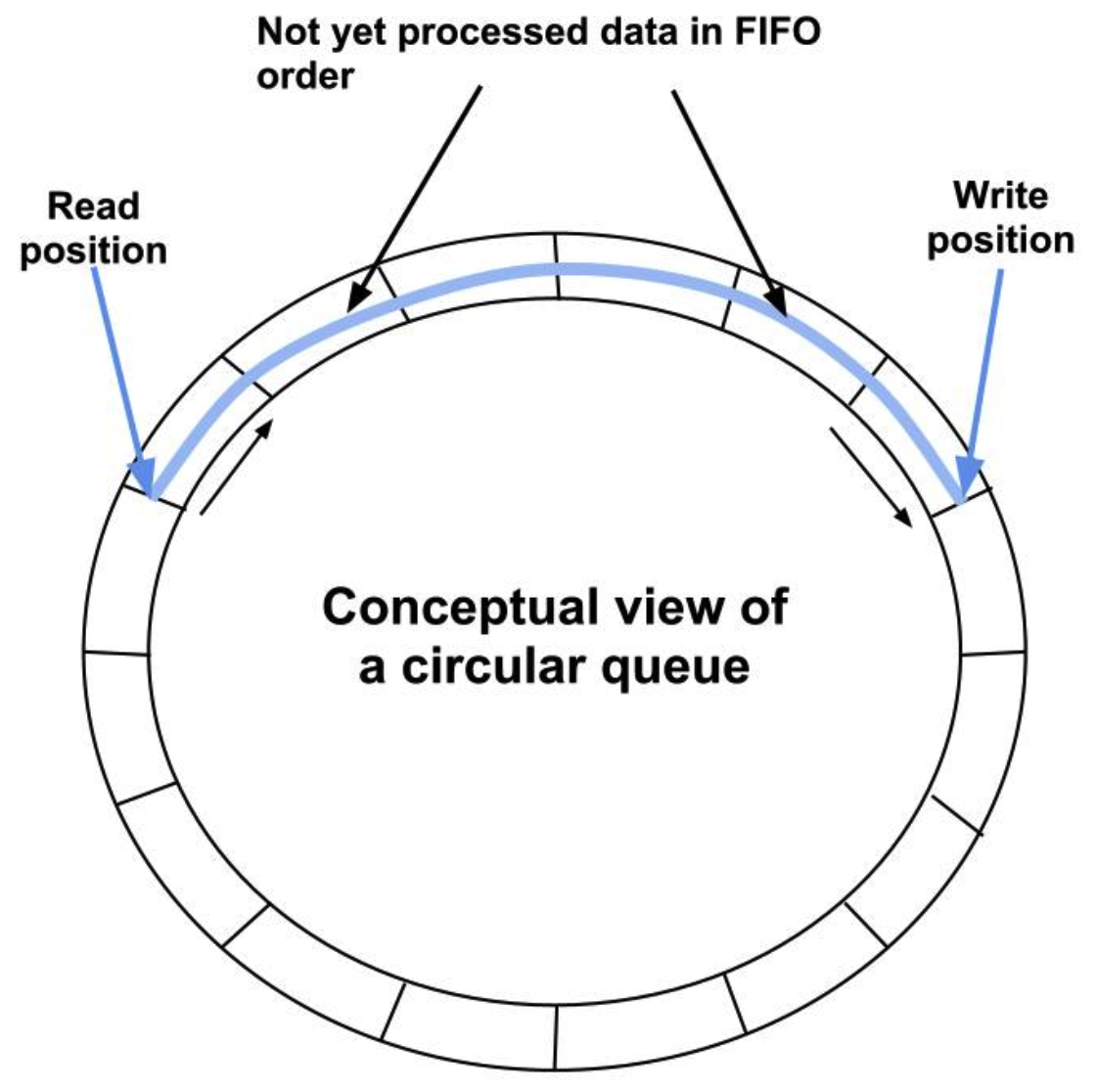
其中一个特性就是GCC 支持的编译器分支预测 __builtin_expect 宏，作为编译分支时候的暗示。这个特性在 linux 的内核代码中很常用，用来提升代码执行速度。

具体的，是有 likely 和 unlikely 这两个宏定义

1 2	#define likely(x) __builtin_expect(!!(x), 1) #define unlikely(x) __builtin_expect(!!(x), 0)

实际使用时，我们可以在很大可能执行的分支前面加上 likely。例如下例中

#include <stdio.h>

#define likely(x) __builtin_expect(!!(x), 1)
#define unlikely(x) __builtin_expect(!!(x), 0)

int main()
{
    int a;
    scanf("%d", &a);
    if (likely(a))
    {
        printf("Hula!\n");
    }
    else
    {
        printf("Woo~\n");
    }
    return 0;
}

这样，如果 likely 所在的分支如果有非常大可能执行，则程序运行效率要比普通的分支判断高。具体原因是什么呢？这就涉及到 CPU 流水线作业的相关知识。

CPU 流水线

这里我们以 Intel 发明的 X86结构的 CPU 为例来大致讲述下 CPU 流水线技术的演进。

CPU 在执行程序的时候依赖于很多寄存器，例如通用寄存器、段寄存器、索引寄存器等。此外还有一个很重要的寄存器：指令指针(IP)。指令指针寄存器是一个拥有特殊功能的指针。指令指针的功能是指向将要运行的下一条指令。

所有的X86处理器都按照相同的模式运行。首先，根据指令指针指向的地址取得下一条即将运行的指令并解析该指令（译码）。在译码完成后，会有一个指令的执行阶段。有些指令用来从内存读取数据或者向内存写数据，有些指令用来执行计算或者比较等工作。当指令执行完成后，这条指令会通过退出(retire)阶段并将指令指针修改为下一条指令。

译码，执行和退出的分阶段模式组成了X86处理器指令执行的基本模式。从最初的8086处理器到新的酷睿i7处理器都基本遵循了这样的过程。

1989年 i486引入了五级流水线模式，分别是：取指(Fetch)，译码(D1, main decode)，转址(D2, translate)，执行(EX, execute)，写回(WB)。之前的三级模式，并不是流水线，每一条指令必须等待前一条指令执行完退出之后才能继续执行。而这种新引入的五级流水线模式，可以同时运行多条指令，每一级流水线在同一时刻都运行着不同的指令。这个设计使得i486比同频率的386处理器性能提升了不止一倍。五级流水线中的取指阶段(F)将指令从指令缓存中取出；第二级为译码阶段(D1)，将取出的指令翻译为具体的功能操作；第三级为转址阶段(D2)，用来将内存地址和偏移进行转换；第四级为执行阶段(EX)，指令在该阶段真正执行运算；第五级为退出阶段(WB)，运算的结果被写回寄存器或者内存。由于处理器同时运行了多条指令，大大提升了程序运行的性能。

流水线化通过同时执行一系列操作增加了吞吐量(throughput)，但是她并没有减少延迟，即并没有减少一条指令从执行开始到执行结束的时间，仍要等到这一系列指令完成。实际上,流水线化由于将一条指令拆分成了几个步骤从而可能会增加延迟。

CPU 分支猜测

流水线技术的主要目的就是通过重叠连续指令的步骤来提高吞吐量从而获得性能，要做到这一点，就必须能够实现确定要执行指令的序列和先后顺序，这样才能使流水线中充满了待执行的指令。当处理器遇到分支条件跳转时，通常不能确定执行那个分支，因此处理器采用分支预测器来猜测每条跳转指令是否会执行。如果猜测比较可靠，那么流水线中就会充满指令。但是，如果对跳转的指令猜测错误，那么就要要求处理器丢掉它这个跳转指令后的所有已做的操作，然后再开始用从正确位置处起始的指令去填充流水线，可以看到这种预测错误会导致很严重的性能惩罚，会导致大约20-40个时钟周期的浪费，从而导致性能的严重下降。

一个很直观的说明 CPU 的分支预测器的例子是 stackoverflow 上的提问： Why is processing a sorted array faster than an unsorted array?

一段排序和未排序过的代码执行速度差别很大，具体代码如下

#include <algorithm>
#include <ctime>
#include <iostream>
int main()
{
    // generate data
    const unsigned arraySize = 32768;
    int data[arraySize];
    for (unsigned c = 0; c < arraySize; ++c)
        data[c] = std::rand() % 256;
    
    //排序这行不注释掉下面的for循环会快得多
    std::sort(data, data + arraySize); 
    
    // test
    clock_t start = clock();
    long long sum = 0;
    for (unsigned i = 0; i < 100000; ++i) {
        // primary loop
        for (unsigned c = 0; c < arraySize; ++c) {
            if (data[c] >= 128)
                sum += data[c];
        }
    }
    double elapsedTime = static_cast<double>(clock() - start) / CLOCKS_PER_SEC;
    std::cout << elapsedTime << std::endl;
    std::cout << "sum = " << sum << std::endl;
}

我在我的 Mac 上运行的结果分别是

1
2
3

# 未排序
21.3109
sum = 312426300000

1
2
3

# 排序后
6.30532
sum = 312426300000

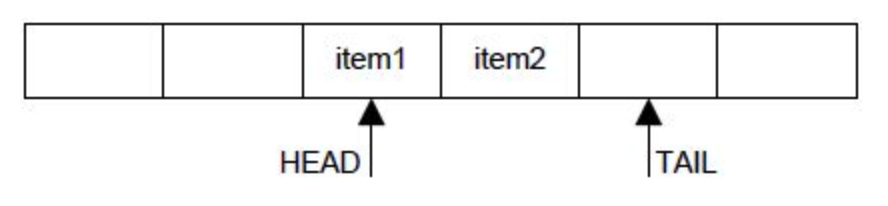
这里影响代码执行的主要片段是

1 2	if (data[c] >= 128) sum += data[c];

对于这段分支代码的执行，CPU 会启用分支预测(branch prediction)，排序和未排序的不同正是分支预测是否有大概率命中。对于命中的情况，CPU 指令可以一路顺畅的执行；而对于预测失败的情况，处理器要flush掉pipelines，回滚到之前的分支，然后重新热启动，选择另一条路径，这里的性能损失非常大。

那么一般怎么做分支预测呢？答案就是根据历史结果来做决定。对于排序的情况，很容易根据历史结果做出决策:

T = branch taken
N = branch not taken

data[] = 0, 1, 2, 3, 4, ... 126, 127, 128, 129, 130, ... 250, 251, 252, ...
branch = N  N  N  N  N  ...   N    N    T    T    T  ...   T    T    T  ...

       = NNNNNNNNNNNN ... NNNNNNNTTTTTTTTT ... TTTTTTTTTT  (easy to predict)

而如果未排序的数组，则其取到的结果完全随机，分支预测基本无效

data[] = 226, 185, 125, 158, 198, 144, 217, 79, 202, 118,  14, 150, 177, 182, 133, ...
branch =   T,   T,   N,   T,   T,   T,   T,  N,   T,   N,   N,   T,   T,   T,   N  ...

       = TTNTTTTNTNNTTTN ...   (completely random - hard to predict)

代码优化

上面说的 CPU 分支预测是属于硬件层面，其实从上层的软件或者程序员角度也是可以协助做好分支预测的。还是回到我们最开始提到的__builtin_expect 宏，示例代码反汇编得到的代码如下

.LC1:
    .string "Hula!"
.LC2:
    .string "Woo~"
 
    call    __isoc99_scanf
    movl    28(%esp), %eax
    testl   %eax, %eax
    je  .L2
    movl    $.LC1, (%esp)
    call    puts
.L3:
    xorl    %eax, %eax
    leave
    ret
.L2:
    movl    $.LC2, (%esp)
    call    puts
    jmp .L3

对于使用了 likely 的分支，其指令将更靠近 testl 分支判断，CPU 在执行分支判断指令的同时，将预先取出后续指令进行执行，而另一个分支指令则需要进行跳转(je .L2)。其本质是优化 CPU 的指令顺序，提高流水线的执行效率。

此外，编写代码时，我们也要注意分支的先后顺序，尽量将概率大的分支放在前面，尽量合并分支，尽量使用排序后的数据来判断，适当使用 goto 和 do while 来优化代码组织等。

参考资料

CPU流水线的探秘之旅

深入理解CPU的分支预测(Branch Prediction)模型

如何在 C++ 代码中提示编译器某个分支的执行概率高？

无锁队列

发表于 2018-08-14 |

引子

无锁队列是一种广泛使用的数据结构

单读单写

我们先看下最简单的一种情况，就是一个生产者负责写，一个消费者负责读的情况。

这种情况通常是利用环形缓冲区 RingBuffer （有时候也称为 circular queue）来实现，那首先看看 RingBuffer 是怎么实现读写的。

RingBuffer 实现

一个数组buff，大小是 SIZE，两个指针变量 head 和 tail 来表示队列的头和尾。写的时候，控制 tail 加1；读的时候，控制 head 加1。

初始状态，数组为空，tail 和 head 都为 0
写入元素时，tail 加1向后更新
读取元素时，head 加1向后更新
由于数组大小size有限，tail 或者 head指针不能永远向后增加，当到达数组尾部（指向size-1）的时候，需要绕回到数组开头，实现的时候使用 val = (val + 1) % size 取余即可
绕回的机制正是环形缓冲的特色，因此 head 和 tail 的前后关系可能会一直变化
队列为空时，读取失败，此时 head 和 tail 相等
队列满时，写入失败，规定如果 tail + 1后，做可能的回绕，然后检查 tail 和head 是否相等，如果相等则满。这种约定浪费了一个元素的位置不让写入，从而保证写满时，head 和 tail差一个元素而不是相等，和队列为空的情况区分开来。此时的情况是可能是
1. tail 在前，head 在后且为 0， tail - head = size - 1 ，此时队列里除最后一个元素外全满，tail + 1 回绕后和head 都为 0
2. head 在前，tail 在后，且 head - tail = 1，tail 加1后和 head 相等

PUSH

POP

EMPTY

FULL

下面看下实现代码

#ifndef PKIT_RING_BUFFER_H_
#define PKIT_RING_BUFFER_H_

template<typename T, int Size>
class RingBuffer{
public:
    enum { Capacity = Size+1 };

    RingBuffer() : _tail(0), _head(0){}
    virtual ~RingBuffer() {}

    bool push(const T& item){
        auto nextTail = increment(_tail);
        if (nextTail == _head) {
            return false;   //full
        }
        _array[_tail] = item;
        _tail = nextTail;
        return true;
    };
    bool pop(T* item){
        if (_head == _tail) {
            return false; //empty
        }
        *item = _array[_head];
        _head = increment(_head);
        return true;
    };

private:
    int increment(int idx) const {
        return (idx + 1) % Capacity;
    };

    int _tail;
    int _head;
    T   _array[Capacity];
};

#endif //PKIT_RING_BUFFER_H_

原子性

现在回到初始的单读单写的情况，生产者调用 push() 来唯一控制 tail 的更新，而消费者调用 pop() 来唯一控制 head 的更新。
实际实现时，通常分步，写入（或读取）缓冲区内容，更新指针。我们要保证：

对 tail 和 head 指针的更新必须是原子的
读的时候，先读取缓冲区内容，再更新 head
写的时候，先写入内容到缓冲区，再更新 tail

关于 int 类型赋值的原子性，C++ 标准是没有定义的，依赖于编译器的实现和系统架构的内存对齐策略等。

根据 KjellKod.cc 的文章的说法，大部分现代处理器上，对于自然对齐的基础类型的读写是原子的，不会出现读一半或者写一半的情况。对于 x86 和 x64 平台，长度大于8的类型，其读写不保证是原子的。而对于我们的 head 和 tail，在 32 位处理器和 64 位处理器上大小分别是 4 和 8 (注：int 的大小和平台和编译器实现有关，这里说法不准) ，因此可以保证是原子的。其英文原话是

On almost all modern processors, reads and writes of naturally aligned native types are atomic. This means that as long as the memory bus is at least as wide as the type being read or written the CPU reads and writes will happen in a single bus transaction. This makes it impossible for other threads to see them half-completed.

For x86 and x64 platforms, types larger than 8 bytes are not guaranteed to be atomic. But in our example the head and tail indexes are integers of size 32bits (4 bytes) on 32-bit processor or 64bits (8bytes) on a 64-bit processor, thus making reading and writing them atomic.

// Example of integers
counter++;                // 1. not atomic operation, but three operations
counter = 0;              // 2. this write is atomic
other_variable = counter; // 3. this read is atomic

For fun, you can compile the operations above to assembly language or use the debugger to view the disassembly. You should then see that the actual store only takes one instruction.

On multiple core CPUs, this is also true. A word in memory must be coherent between all cores when it is written (using one CPU instruction). It is simply not allowed or even possible to split a 4 byte writing (I use a 32-bit example) between cores, since a word (4 bytes) is written as a single instruction.

In short. Reads and writes of tail and head are atomic. First is still OK.

保险的措施是使用c++11中的 std::atomic 来保证原子性。我们修改下 head 和 tail 定义后的 ssqueue 结构(single producer & single consumer queue) 如下

#ifndef PKIT_SSQUEUE_H_
#define PKIT_SSQUEUE_H_

#include <atomic>

template<typename T, int Size>
class SSQueue{
public:
    enum { Capacity = Size+1 };

    SSQueue() : _tail(0), _head(0){}
    virtual ~SSQueue() {}

    bool push(const T& item){
        auto currTail = _tail.load();
        auto nextTail = increment(currTail);
        if (nextTail == _head.load()) {
            return false;   //full
        }
        _array[currTail] = item;
        _tail.store(nextTail);
        return true;
    };
    bool pop(T* item){
        auto currHead = _head.load();
        if (currHead == _tail.load()) {
            return false; //empty
        }
        *item = _array[currHead];
        _head.store(increment(currHead));
        return true;
    };

private:
    int increment(int idx) const {
        return (idx + 1) % Capacity;
    };

    std::atomic<int> _tail;
    std::atomic<int> _head;
    T   _array[Capacity];
};

#endif //PKIT_SSQUEUE_H_

顺序执行

由于都是分步执行，中间有可能被打断。但是只要保证了读写缓冲区的和更新指针的顺序，就能保证无锁的安全性。

现在来分析一下打断的情况：
假如读的时候，消费者先读取了缓冲区内容，而未来得及更新 head，执行权就被生产者抢占，于是生产者读的 head 就是老的，类似快照数据。但这并没有太大影响，顶多是极端情况下由于没有更新head 导致生产者认为队列满而写入失败，下次继续写就可以了；如果队列没满，写入不受影响。
同样的道理，假如写的时候，生产者先写入内容到缓冲区(也可能是写一部分)，而未来得及更新 tail，执行权就被消费者抢占，于是消费者读到的 tail 也是老的。这也没有多大影响，顶多是极端情况下由于没有更新tail导致消费者认为队列空而读取失败，下次继续读就读到数据了；如果队列非空，读取不受影响。

这里特别注意的是，head 和 tail 指针永远只由一方来更新，且是单方向更新。

那是不是代码里先写缓冲区操作，再写更新指针操作就可以了呢？答案是否。

编译器优化我们的代码时，可能会改变代码的执行顺序，反应在汇编指令的前后顺序调整。这是编译时乱序。

上面提到的利用 volatile 修饰的 int 变量，vs 和 gcc 编译器似乎都能保证其汇编指令顺序，但是没有得到权威的资料证明 (查看)

此外，由于现代CPU普遍采用了多级流水线技术，一条指令的执行是多级流水线协同完成。为了提高执行效率，可以同时执行多条指令；而且随着分支预测和乱序执行的引入，互不依赖的两条指令在执行时是不保证先后顺序的，这是运行时乱序。

编译器开发者和cpu厂商都遵守着内存乱序的基本原则，简单归纳如下：

1	不能改变单线程程序的行为

在单线程环境，我们不必关心内存乱序的影响。而此时，我们关注的恰恰是多线程执行的情况，如何保证我们代码的顺序执行就是需要解决的关键问题。

一种方式是依赖 volatile int 的一种实现。

1 2	volatile int head; volatile int tail;

这里特别指出，volatile 关键字语义上只是提示编译器不要优化该变量，本质上和顺序执行没有任何关系。有说法是 volatile 的使用保证读写变量时其汇编指令顺序不会变更，但是没有可靠依据。

而对于执行乱序

CPU Reordering Summary for x86 and x64 Platforms

1. Reads moving ahead of other reads: No
2. Writes moving ahead of other writes: No
3. Writes moving ahead of reads: No
4. Reads moving ahead of writes: Yes

由 2、3 两条保证了写的顺序不被置于读之前，且写之间顺序不乱。

同样，保险的方式还是使用平台无关的机制：c++11提供的内存屏障。

Acquire-Release 内存屏障代码

#ifndef PKIT_SSQUEUE_H_
#define PKIT_SSQUEUE_H_

#include <atomic>

template<typename T, int Size>
class SSQueue{
public:
    enum { Capacity = Size+1 };

    SSQueue() : _tail(0), _head(0){}
    virtual ~SSQueue() {}

    bool push(const T& item){
        auto currTail = _tail.load(std::memory_order_relaxed);
        auto nextTail = increment(currTail);
        if (nextTail == _head.load(std::memory_order_acquire)) {
            return false;   //full
        }
        _array[currTail] = item;
        _tail.store(nextTail, std::memory_order_release);
        return true;
    };
    bool pop(T* item){
        auto currHead = _head.load(std::memory_order_relaxed);
        if (currHead == _tail.load(std::memory_order_acquire)) {
            return false; //empty
        }
        *item = _array[currHead];
        _head.store(increment(currHead), std::memory_order_release);
        return true;
    };

private:
    int increment(int idx) const {
        return (idx + 1) % Capacity;
    };

    std::atomic<int> _tail;
    std::atomic<int> _head;
    T   _array[Capacity];
};

#endif //PKIT_SSQUEUE_H_

http://chonghw.github.io/blog/2016/09/05/compilermemoryreorder/

多读多写

如果情况扩展到多读多写的情况，我们就不能像上面这样来实现了。必须要借助 CPU 提供的 CAS 操作指令。

CAS

Compare & Set，或是 Compare & Swap，现在几乎所有的CPU指令都支持CAS的原子操作，X86下对应的是 CMPXCHG 汇编指令。有了这个原子操作，我们就可以用其来实现各种无锁（lock free）的数据结构。

维基百科是这么说的

1
2

In computer science, compare-and-swap (CAS) is an atomic instruction used in multithreading to achieve synchronization. It compares the contents of a memory location with a given value and, only if they are the same, modifies the contents of that memory location to a new given value. This is done as a single atomic operation. The atomicity guarantees that the new value is calculated based on up-to-date information; if the value had been updated by another thread in the meantime, the write would fail. The result of the operation must indicate whether it performed the substitution; this can be done either with a simple boolean response (this variant is often called compare-and-set), or by returning the value read from the memory location (not the value written to it).
Algorithms built around CAS typically read some key memory location and remember the old value. Based on that old value, they compute some new value. Then they try to swap in the new value using CAS, where the comparison checks for the location still being equal to the old value. If CAS indicates that the attempt has failed, it has to be repeated from the beginning: the location is re-read, a new value is re-computed and the CAS is tried again.

使用 c 代码形象的来表示这个操作就是

bool compare_and_swap(int *accum, int *dest, int newval)
{
  if (*accum == *dest) {
      *dest = newval;
      return true;
  } else {
      *accum = *dest;
      return false;
  }
}

将变量值 accum 与 dest 进行 compare，如果相等则进行 Swap/Set。如果不相等，则返回一个标识值。上层需要重复调用该 CAS 操作，直到操作成功。

C 中使用 CAS

C 语言中使用 CAS，可以使用

C11) <stdatomic.h> 里的一系列函数

_Bool atomic_compare_exchange_strong( volatile A* obj,
                                      C* expected, C desired );
_Bool atomic_compare_exchange_weak( volatile A *obj, 
                                    C* expected, C desired );

特定编译器的非标准 C 扩展

//GCC
bool __sync_bool_compare_and_swap (type *ptr, type oldval type newval, ...)	
type __sync_val_compare_and_swap (type *ptr, type oldval type newval, ...)

//Windows API
InterlockedCompareExchange ( __inout LONG volatile *Target,
                                __in LONG Exchange,
                                __in LONG Comperand);

直接调用compare-and-swap 汇编指令编写的函数。

下面是使用链表实现的基于 CAS 操作的无锁队列

EnQueue(x) //进队列
{
    //准备新加入的结点数据
    q = new record();
    q->value = x;
    q->next = NULL;
 
    do {
        p = tail; //取链表尾指针的快照
    } while(CAS(p->next, NULL, q) != TRUE); //如果没有把结点链在尾指针上，再试
 
    CAS(tail, p, q); //置尾结点
}

DeQueue() //出队列
{
    do{
        p = head;
        if (p->next == NULL){
            return ERR_EMPTY_QUEUE;
        }
    while( CAS(head, p, p->next) != TRUE );
    return p->next->value;
}

ABA 问题

所谓ABA（见维基百科的ABA词条），问题基本是这个样子：

进程P1在共享变量中读到值为A
P1被抢占了，进程P2执行
P2把共享变量里的值从A改成了B，再改回到A，此时被P1抢占。
P1回来看到共享变量里的值没有被改变，于是继续执行。

虽然P1以为变量值没有改变，继续执行了，但是这个会引发一些潜在的问题。ABA问题最容易发生在lock free 的算法中的，CAS首当其冲，因为CAS判断的是指针的地址。如果这个地址被重用了呢，问题就很大了。（地址被重用是很经常发生的，一个内存分配后释放了，再分配，很有可能还是原来的地址）

比如上述的DeQueue()函数，因为我们要让head和tail分开，所以我们引入了一个dummy指针给head，当我们做CAS的之前，如果head的那块内存被DeQueue() 然后回收并被重用了，而重用的内存又被EnQueue()进来了，这会有很大的问题。（内存管理中重用内存基本上是一种很常见的行为）

维基百科上给了一个解——使用double-CAS（双保险的CAS），例如，在32位系统上，我们要检查64位的内容

1）一次用CAS检查双倍长度的值，前半部是指针，后半部分是一个计数器。

2）只有这两个都一样，才算通过检查。然后把指针赋新的值，并把计数器累加1。

总结

无锁队列主要是通过CAS、FAA这些原子操作，和Retry-Loop实现。
对于Retry-Loop，其实和锁什么什么两样。只是这种“锁”的粒度变小了，主要是“锁”HEAD和TAIL这两个关键资源。而不是整个数据结构。

参考资料

Lock-Free Single Producer - Single Consumer Circular Queue 1

Lock-Free Single-Producer - Single Consumer Circular Queue 2

无锁环形队列，volatile和乱序执行

volatile vs. volatile

Why do we use volatile keyword in C++?

C++内存屏障（内存顺序）总结

Memory Barriers Are Like Source Control Operations

无锁队列的实现

tcp/ip备忘

发表于 2018-08-13 |

匹配系统设计

发表于 2018-08-12 |

帧同步实现实时对战

发表于 2018-08-11 |

状态同步

玩家上传操作，服务器做战斗计算，包括技能，移动，AI等，将计算结果广播给所有参与者客户端。客户端只作为表现端。

帧同步

玩家上传操作，服务器只做转发，客户端收到操作指令后，开始战斗逻辑计算及表现。

严格帧锁定

所有客户端完全同步，服务器每一帧等待所有客户端上传：有操作或者无操作，集齐后转发给所有客户端，然后客户端做逻辑计算和表现。

如果由于网络原因导致某些玩家上传消息没有被服务器收到，则帧暂停等待。这种情况下，一卡全卡，体验不太好。

乐观帧锁定

服务器不会等待客户端上传，而是以固定的帧率，例如每秒10帧，给客户端广播玩家操作指令。玩家的操作会确定的落在某一帧内。这样，网速慢的玩家需要不停追帧，但网速好的玩家体验会非常好。

现在的帧同步往往指这一种方式。

日志组件实现

发表于 2018-08-11 |

定时器实现

发表于 2018-08-11 |

定时器是游戏开发中常用的基础组件，本文介绍几种定时器组件的实现方法。

Linux 内核定时器实现

Linux 内核的定时器从1997年之后基本没有修改过，最终版本是使用时间轮算法的定时器。定时器的最大设置超时范围是 2^32 个jiffies。设置 jiffie 为毫秒级或者秒级，就可以控制定时器的精度。例如 jiffie 设置为100ms，即1秒相当于10个jiffie，则定时器的最大范围是

2^32 / 10 / 86400 = 4971 天

该实现主要提供了以下接口添加或者删除定时器：

1 2	timer = add_timer(expire) del_timer(timer)

定时器的超时 expire 被定义位 n 个 jiffies

如果定时器超时，则调用注册的回调函数

1	timer->fn(timer->data)

最初始定时器的实现采用的是最简单的方式，就是将所有的定时器串成一个有序的双向链表。

这种方式添加定时器的方式就是从前往后遍历顺序链表，找到合适的位置插入，时间复杂度是 o(n)；删除定时器则非常简单，是 o(1)复杂度；超时复杂度也是 o(1)。这种定时器的实现方式缺点在与管理大量定时器时，效率不高。

另一种能想到的定时器实现方式，是使用二叉排序树。左子树的超时时间比右子树的超时时间小，于是每次添加定时器时只需要二分查找，因此复杂度是 o(log(N))；删除和超时则是 o(1)；

还有一种方式，就是申请 2^32个桶，然后每个桶中维护一个 list 用来存放定时器，而每个 jiffie 对应一个桶，定时器的插入操作就是简单的索引到桶，然后执行 list_add() 操作，时间复杂度变为 o(1)；同样的，删除和超时都是 o(1) 操作。其实这就是最初版本的基于时间轮的算法，如下图所示

这种方式时间复杂度是最低的，但是其需要的内存空间巨大，尤其是在定时器数量不多的时候，是个很大的浪费。

那么，有没有一种方式是对这种桶方式的改进，能同时满足时间复杂度和空间复杂度呢？这就是目前采用的多精度时间轮算法。多精度有种很形象的比喻，就是平时看到的水表

在上面的水表中，为了表示度量范围，分成了不同的单位，比如 1000，100，10 等等，相似的，表示一个 32bits 的范围，也不需要 2^32 个元素的数组。

具体实施时，将所有的 jiffie 分成5组：

1	1..256, 257..16384, 16385..1048576, 1048577..67108864, 67108865..4294967295

第一组，就是即将到期的256个jiffie，为每个 jiffie 分配一个桶(bucket)，一共是256个桶。这里每个桶里定时器的到期时间都是相同的，精度为1jiffie。

第二组，我们分为64个桶，每个桶里存放接下来到期的256个 jiffie 对应的定时器。在这里，可以看到桶里定时器的到期时间是不同的，也就是精度是256 jiffies。

第三组，还是分为64个桶，于是每个桶的精度就是 256 * 64 = 16384 jiffies。

第四组，还是分为64个桶，每个桶的精度是 256 64 64 = 1048576 jiffies。

最后一组，依旧分为64个桶，每个桶的精度是 256 64 64 * 64 = 67108864 jiffies。

最终我们用到的桶的数量是 256+64+64+64+64 = 512 buckets。也就是说我们通过控制桶的精度，将2^32个 jiffies (32 bits) 分成了 8 + 6 + 6 + 6 + 6 bits 。可能有人问了，为什么这么分呢，为什么不是 8 + 8 + 8 + 8 ? 从作者的回复来看，主要是 256 + 256 + 256 + 256 = 1024个桶，这比512个桶空间占用多。

那么如何插入定时器呢？首先根据定时器的 expire 来定位到放到哪一组中，然后再定位到具体的桶 index。注意，除了第一组之外其他组的桶中，定时器的到期时间都可能是不同的。例如到期时间分别是 260 jiffies 和 265 jiffies 的定时器都会被放入第二组的第一个桶中( 257 jiffies ~ 512jiffies 都在这个桶中)。这表示这些桶中的定时器是『部分排序的』，本质上是对他们的高位进行排序。插入定时器的操作只是定位到具体的桶 index，然后执行 list_add() 操作(链表本身不需要排序)，时间复杂度是 o(1)；而删除也是一样定位组和桶 index，时间复杂度 o(1)。

问题是怎么执行定时器的超时呢？第一组里的256个桶没有问题，我们只需要在时间轮的指针逐次增加1并指向对应的 jiffies 时，执行其对应桶里的所有定时器即可。那如果指针指向第 257 jiffie 呢？从前面的分析我们可以知道，第 257 jiffie 指向的桶里可能包含 257 jiffies ~ 512 jiffies 这 256个 jiffies 的定时器，它们是非顺序地存储在桶的链表内，不能直接执行。执行前，需要做的就是将这个桶里的所有定时器全部重新映射到第一组的256个桶里，即将粗精度的定时器重新进行细精度的划分/排序。由于时间指针已经指向第257 jiffies，那么第二组第一个桶里的所有定时器的相对超时时间必定都减少了256 jiffies，因为重新添加时，会落到第一组的细精度桶区间内。同样的过程，我们在指针指向第三组 (16385jiffies ~ 1048576jiffies) 的定时器时，将这组里各桶的定时器重新添加映射到前面两组的桶内。后面各组的执行也类似。

重新添加/映射完成之后，每次我们只用执行相对于定时器指针相差 256个 jiffies 的定时器(也就是总是执行第一组里的定时器)，如果超过256则再继续执行重新添加/映射，再执行映射后的第一组，如此循环。

本质上，这种策略称为一种『延迟排序』，即定时器在很久到期时，我们对其进行粗粒度的排序，即只排序高位，就是定位放入哪个桶即可，从而提高效率。而当快要执行时，才将其进行细粒度排序及定位。这带来一个很明显的好处是，如果定时器不执行(即到期前就被删除)，由于添加和删除的时间复杂度都是 o(1)，其效率将非常高。

在定时器的实际使用时，很多确实是没有到期即被删除。可以想像下大量防止网络超时的定时器。

最小堆定时器

最小堆也是实现定时器的一种常用方式，例如 libevent 库的定时器就是使用的最小堆优先级队列。Golang 官方库中的 timer 也是使用的最小堆原理。

所谓最小堆，其实是一颗特殊的二叉树，其所有节点的值都比左右子节点的值要小。因此整个二叉树的最小值就在 root 元素。每次检查定时器是否到期时，我们检查 root 元素是否到期即可。同时，这棵二叉树又是一个完全二叉树。如果一棵二叉树除了最右边位置上一个或者几个叶结点缺少外其它是填满的，那么这样的二叉树就是完全二叉树。严格的定义是：若设二叉树的高度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层从右向左连续缺若干结点，就是完全二叉树。下面这几颗二叉树都是完全二叉树

其基本类似于下面这个形状：

那如何表示一颗完全二叉树呢？只需要一个数组即可。首先将完全二叉树进行从上到下，从左到右编号：

通过上图我们发现如果完全二叉树的一个父结点编号为 k，那么它左儿子的编号就是 2k，右儿子的编号就是 2k+1。如果已知儿子（左儿子或右儿子）的编号是 x，那么它父结点的编号就是 x/2，注意这里只取商的整数部分。在 C 语言中如果除号‘/’两边都是整数的话，那么商也只有整数部分（即自动向下取整），即 4/2 和 5/2 都是 2。另外如果一棵完全二叉树有 N 个结点，那么这个完全二叉树的高度为 log2 N 简写为 log N，即最多有 log N 层结点。

如果我们现在想添加一个定时器，也就是新增一个节点(例如值为3)，该如何操作呢？只需要直接将新元素插入到末尾，再根据情况判断新元素是否需要上移，直到满足堆的特性为止。如果堆的大小为 N（即有 N 个元素），那么插入一个新元素所需要的时间也是 O(logN)。

先将 3 与它的父结点 25 比较，发现比父结点小，为了维护最小堆的特性，需要与父结点的值进行交换。交换之后发现还是要比它此时的父结点 5 小，因此需要再次与父结点交换。至此又重新满足了最小堆的特性。

向上调整的代码如下

void siftup(int i) //传入一个需要向上调整的结点编号i
{
    int flag=0; //用来标记是否需要继续向上调整
    if(i==1)  return; //如果是堆顶，就返回，不需要调整了    
    //不在堆顶 并且 当前结点i的值比父结点小的时候继续向上调整 
    while(i!=1 && flag==0)
    {
        //判断是否比父结点的小 
        if(h[i]<h[i/2])
            swap(i,i/2);//交换他和他爸爸的位置 
        else
            flag=1;//表示已经不需要调整了，当前结点的值比父结点的值要大 
        i=i/2; //这句话很重要，更新编号i为它父结点的编号，从而便于下一次继续向上调整 
    }
}

定时器到期又是如何处理呢？根据最小堆的特性，先到期的就是 root 节点，因此执行定时器函数后，我们将 root 元素删除，同时将堆的最后一个节点移动到 root 位置，然后看是不是需要执行向下调整，以保持最小堆的特性。

向下调整的代码如下

void siftdown(int i) //传入一个需要向下调整的结点编号i，这里传入1，即从堆的顶点开始向下调整 
{
    int t,flag=0;//flag用来标记是否需要继续向下调整 
    //当i结点有儿子的时候（其实是至少有左儿子的情况下）并且有需要继续调整的时候循环窒执行
    while( i*2<=n && flag==0 )
    {        
        //首先判断他和他左儿子的关系，并用t记录值较小的结点编号 
        if( h[i] > h[i*2] )
            t=i*2;
        else
            t=i; 
        //如果他有右儿子的情况下，再对右儿子进行讨论 
        if(i*2+1 <= n)
        {
            //如果右儿子的值更小，更新较小的结点编号  
            if(h[t] > h[i*2+1])
                t=i*2+1;
        }
        //如果发现最小的结点编号不是自己，说明子结点中有比父结点更小的  
        if(t!=i)
        {
            swap(t,i);//交换它们，注意swap函数需要自己来写
            i=t;//更新i为刚才与它交换的儿子结点的编号，便于接下来继续向下调整 
        }
        else
            flag=1;//则否说明当前的父结点已经比两个子结点都要小了，不需要在进行调整了 
    }
}

同样的，如果要在定时器到期之前删除它，就类似于删除最小堆的任一节点。方式是将最后一个节点放置到该删除的节点，然后从该节点开始执行向下调整，直到整个堆又满足最小堆的特性，本质上和定时器到期时删除 root 节点的思路是一致的。时间复杂度也是 O(logN)。

参考资料

Linux 下定时器的实现方式分析

kernel timer design

极客时间：二叉树

游戏中的加密应用

发表于 2018-08-03 |

游戏中加密算法的选择

前面一篇文章我们已经介绍了对称解密算法和非对称加密算法，那在游戏协议通信中应该如何选择加密方式呢？

那我们看看下列几个方案

单独使用对称加密算法。典型的对称加密算法如 AES 安全性已经不错，而且加密效率高，似乎可以直接拿来使用。但问题是客户端和服务器交互时如何交换密钥？如果直接明文传输，肯定会有被嗅探的风险。所以单独使用对称加密算法存在密钥的管理问题，是不可行的。
单独使用非对称加密算法。非对称加密算法基于未解决的数学难题，因此在破解上几乎不可能。其优点就是安全，但缺点就是不够快，比较耗费cpu，如果在游戏中每一次消息都用其加密，对cpu的损耗还是挺高的。

一种折中的办法是：采用密钥交换算法交换对称加密算法的密钥，然后用对称加密算法加密数据。

所谓密钥交换，通俗地说，即使有攻击者在偷窥你与服务器的网络传输，客户端（client）依然可以利用“密钥协商机制”与服务器端（server）协商出一个用来加密应用层数据的密钥（也称“会话密钥”）。

那么如何进行安全的密钥交换呢？

一种方案是使用非对称加密算法。原理是通信一方首先生成密钥对，私钥自己保存，然后将公钥发送给另外一方；另一方拿到公钥后，随机生成一个对称加密的密钥，然后利用公钥加密它；再把加密结果发给对方，对方用私钥解密；于是双方都得到了会话密钥。后续通信就使用该密钥进行对称加解密。例如早期的 SSLv2只支持一种密钥协商方式，就是基于RSA 非对称加密算法的密钥协商机制。
第二种方案是使用专用的密钥交换算法，如 DH算法及其改进型 ECDH算法。该交换算法比较复杂，我们在后面的内容中进行介绍。
还有一种方案就是基于 PSK的密钥协商。PSK 全称Pre-Shared Key，顾名思义，就是预先让通讯双方共享一些密钥（通常是对称加密的密钥）。所谓的预先，就是说，这些密钥在 TLS 连接尚未建立之前，就已经部署在通讯双方的系统内了。其具体步骤是在通讯之前，通讯双方已经预先部署了若干个共享的密钥。为了标识多个密钥，给每一个密钥定义一个唯一的 ID。协商的过程很简单：客户端把自己选好的密钥的 ID 告诉服务端。如果服务端在自己的密钥池子中找到这个 ID，就用对应的密钥与客户端通讯；否则就报错并中断连接。

最后一种方式考虑到所有会话都使用这些固定的密钥，比较少用到。我们只看前两种方式。

DH 系交换算法

DH 算法

DH，全称Diffie–Hellman key exchange，是一种安全协议。它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥。这个密钥可以在后续的通讯中作为对称密钥(通过对称加密算法)来加密通讯内容。

其基本原理如下

如果 p 是一个至少 300 位的质数，并且a和b至少有100位长，那么即使使用全人类所有的计算资源和当今最好的算法也不可能从g, p和ga mod p 中计算出 a。这个问题就是著名的离散对数问题。注意g则不需要很大, 并且在一般的实践中通常是2或者5。

密钥交换的流程主要有2步：

初始化密钥对，并向对方公布自己的公钥
构建本地密钥，作为后续加密的密钥

以消息传递模型为例，甲方为发送者，乙方为接收者，分述甲乙双方如何构建密钥，交换密钥和加密数据。

首先，甲乙双方需要在收发信息前构建自己的密钥对，如下图：

注意，乙方构建自己的密钥对必须使用甲方公钥作为参数，否则无法确保甲乙双方获得同一个私密密钥，消息加密更无从谈起。其次，假设甲乙双方事先约定好了用于数据加密的对称加密算法（如 AES 算法），并构建本地密钥（即对称加密算法中的密钥），甲方需要使用自己的私钥和乙方的公钥才能构建本地密钥，即用于数据加解密操作的对称加密算法密钥。同样，乙方需要使用自己的私钥和甲方的公钥构建本地密钥。如下图：

虽然甲乙双方使用了不同的密钥来构建本地密钥，但得到的密钥是一致的，正因为如此，甲乙双方才能顺利进行加密消息的传递。最后，甲乙双方构建了本地密钥后，可按基于对称加密算法的消息传递模型完成消息传递，如下图：

ECDH算法

DH 算法有一个变种，称之为 ECDH（全称是“Elliptic Curve Diffie-Hellman”）。

它与 DH 类似，差别在于： DH 依赖的是——求解“离散对数问题”的难题。 ECDH 依赖的是——求解“椭圆曲线离散对数问题”的难题。其密钥交换过程于 DH 算法基本一致，这里我们不在赘述。

PFS 特性的保证

PFS 全称perfect forward secrecy，中文翻译叫『完美前向保密』，是由Christoph G. Günther在EUROCRYPT ’89提出的，其最初用于定义会话密钥交换协议的一种安全性。通俗点解释，就是如果当前会话的密钥协商私钥被破解，只能影响当前会话，不能影响之前历史会话。

对于 RSA 密钥协商来说，如果服务器维护的的私钥被破解，则之前所有历史会话中的加密密钥都被破解了。当然你也可以说，服务器为每次会话都产出一对用来协商的密钥对，但是这个生成过程往往比较耗费资源。

而 DH 算法及其衍生 ECDH 算法，每次会话的密钥交换都是临时生成的密钥对，完全满足 PFS 的要求，且其生成过程相对于 RSA 算法要廉价的多。

综上，我们更倾向于使用 ECDH+AES 的算法组合。

具体选择时，我们可以考虑

对称加密我们可以使用 AES-128 或者 XXTea 算法。
密钥交换使用ECDH算法。

中间人攻击

中间人攻击（英语：Man-in-the-middle attack，简称MITM）是指攻击者与通讯的两端分别创建独立的联系，并交换其所收到的数据，使通讯的两端认为他们正在通过一个私密的连接与对方直接对话，但事实上整个会话都被攻击者完全控制。在中间人攻击中，攻击者可以拦截通讯双方的通话并插入新的内容。在许多情况下这是很简单的（例如，在一个未加密的Wi-Fi的接受范围内的中间人攻击者，可以将自己作为一个中间人插入这个网络）。

一个中间人攻击能成功的前提条件是攻击者能将自己伪装成每一个参与会话的终端，并且不被其他终端识破。中间人攻击是一个（缺乏）相互认证的攻击。其大致过程如下图所示

目前，单纯的 ECDH + AES 算法是无法防止中间人攻击的，为此就需要引入身份认证机制，其中使用最多的就是数字认证机制，也就是 CA 证书，这也是目前广泛使用的 Https 协议（本质上是基于 TLS 加密协议）使用的方式。

所谓 CA，即Certificate Authority，就是颁发数字证书的权威机构，充当『公证人』的角色。服务器拿到 CA 颁发的证书，就认为是可以被客户端信赖的，客户端确认了服务器的有效身份，后续的密钥协商和加密通信就可以认为是安全的。

目前常用的数字签名算法有 DSA，RSA，ECDSA(基于 ECC 的 DSA)，其大致原理就是服务器使用私钥对一段信息进行签名(加密)，然后客户端拿到签名时候，使用公钥进行验证(解密)，如果通过，就认为签名有效。

大致原理如下：

第1步
服务器方面首先要花一笔银子，在某个 CA 那里购买一个数字证书。
该证书通常会对应几个文件：其中一个文件包含公钥，还有一个文件包含私钥。必须在服务器上部署这两个文件。

第2步
当客户端访问时，服务器首先把包含公钥的证书发送给它。

第3步
客户端验证服务器发过来的证书。如果发现其中有诈，则退出。
由于有了这一步，就大大降低了“中间人攻击”的风险。

为啥客户端（典型的如 https 协议一方的浏览器）能发现 CA 证书是否有诈？
因为正经的 CA 证书，都是来自某个权威的 CA。如果某个 CA 足够权威，那么主流的操作系统（或浏览器）会内置该 CA 的“根证书”。（比如 Windows 中就内置了几十个权威 CA 的根证书）
因此，客户端就可以利用系统内置的根证书，来判断服务器发过来的 CA 证书是不是某个 CA 颁发的。

第4步
如果服务器的 CA 证书没有问题，那么客户端就从该 CA 证书中提取出“公钥”。
然后浏览器随机生成一个“对称加密的密钥”（以下称为 k）。用 CA 证书的公钥加密 k，得到密文 k'，然后把 k' 发送给服务器。

第5步
服务器收到客户端发过来的 k'，用之前保存的私钥进行解密，得到 k。
至此，客户端和服务器都拥有 k，“密钥交换”大功告成啦。

目前来说，数字签名算法+密钥协商算法+对称加密算法的组合相对来说是一种比较安全的加密通信方式，再加上 HMAC 进行摘要完整性校验，可以说能应付大部分普通攻击了。
而通常游戏中返回给客户端进行交互的服务器地址一般是可信赖的服务器 ip 列表，因此目前来说没有使用数字证书来防止中间人攻击的必要。因此此前提到的『密钥协商算法+对称加密算法』组合在游戏通信中得到了普遍应用。

参考资料

密钥交换（密钥协商）算法及其原理

图解SSL/TLS协议

密码学算法简介

发表于 2018-07-28 |

前言

本文主要介绍常用的加解密算法。常用的算法大致分为以下几类：

哈希算法
古典加密
对称密钥加密
非对称密钥加密

哈希算法

常用的哈希算法，可以对任意长度的报文计算出固定长度的摘要，俗称哈希值。哈希值相对于原文来说要简短的多，往往只有十几或者几十个字节，因此也称为摘要算法。这个计算过程理论上是单向不可逆的：从报文可以计算出摘要，但是从摘要无法逆向计算出原始的报文。

哈希算法的一个重要应用就是加密密码，加密后的密码无法被逆向反推，从而达到受保护的目的。在校验密码时，我们只需要比对哈希后的值即可。

此外，哈希算法还可以用来校验完整性。例如很长一段信息或者下载获得一份文件，怎么能保证就是原始的信息或者文件呢？我们只需要对比传输前后信息的哈希值或者下载文件和原始文件的哈希值即可确定是否完整。

哈希算法(信息或文件) = 摘要或哈希值

SHA-1

SHA-1（Secure Hash Algorithm 1）是一种密码哈希函数，美国国家安全局设计，并由美国国家标准技术研究所发布为联邦数据处理标准。SHA-1可以生成一个被称为消息摘要的160比特位( 20字节 )散列值，散列值通常的呈现形式为40个十六进制数。

SHA-1目前已经不够安全，已经有很多有效攻击的手段，因此正在被减少使用。

SHA-2

SHA-2 属于SHA-1算法的后继者。其下又可再分为六个不同的算法标准，包括了：SHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256。后面的数字代表了最后摘要值的比特位数。

SHA-2的密码安全性目前还未得到广泛信任，有待进一步验证。SHA-256( 32字节 )算法目前已经被 TLS1.2标准采用。

MD5

MD5消息摘要算法（Message-Digest Algorithm），一种被广泛使用的密码散列函数，可以产生出一个128位（ 16字节 ）的散列值（hash value）。

2009年，中国科学院的谢涛和冯登国用了很小的碰撞算法复杂度，破解了MD5的碰撞抵抗，该攻击在普通计算机上运行只需要数秒钟。因此，对于需要高度安全性的数据，专家一般建议改用其他算法，如SHA-2系列算法。

暴力破解

使用哈希算法保护的密码目前已经很容易被暴力破解，其中就采用了一种称为 table 的技术。黑客们发现如果能够实现直接建立出一个数据文件，里面事先记录了采用和目标采用同样算法计算后生成的Hash散列数值，在需要破解的时候直接调用这样的文件进行比对，破解效率就可以大幅度地，甚至成百近千近万倍地提高，这样事先构造的Hash散列数据文件在安全界被称之为Table表(文件)。最出名的Tables是Rainbow Tables，即安全界中常提及的彩虹表。正是由于Rainbow Tables的存在，使得普通电脑在5分钟内破解14位长足够复杂的Windows帐户密码成为可能。

针对彩虹表之类的暴力破解方式，可以采用的方法就是添加多字节随机盐及多次哈希，增加破解建表的难度，从而提升密码相对安全性。例如

1	saltedhash(password) = hash(password \|\| salt)

或者

1	saltedhash(password) = hash(hash(password) \|\| salt)

推荐使用 bcrypt 或者 PBKDF2 加盐哈希算法。

古典加密

古典加密是历史上使用过的加密信息的算法，其大部分加密方式都是利用替换式密码或移项式密码，有时则是两者的混合。其于历史中经常使用，但现代已经很少使用，大部分的已经不再使用了。许多密码起源于军事上，相同立场的人常使用来寄送秘密讯息。经典的方法常攻击密码文，有时候甚至不知其密码系统，也可以使用工具，像是频率分析法。有些经典密码是使用先进的机器或是机电密码机器，像是恩尼格玛密码机。

经典密码通常很容易被破解。许多经典密码可单单经由密文而破解，用暴力破解或者频率分析可以轻而易举的攻破这些加密算法。

替换式密码

凯撒密码是广为人知的代换密码。为了用凯撒密码法加密讯息，每个密码字母集中的字母将会被其位置的后3个字母替代。因此字母A将会被字母D替代、字母B将会被字母E替代、字母C将会被字母F替代等，最后，X、Y和Z将分别的被替代成A、B和C。例如，”WIKIPEDIA”将被加密成”ZLNLSHGLD”。凯撒把字母向后移”3”位，但其他数字也可照著作。

移位式密码

移位式密码，它们字母本身不变，但它们在讯息中顺序是依照一个定义明确的计划改变。许多移位式密码是基于几何而设计的。一个简单的加密（也易被破解），可以将字母向右移1位。例如，明文”Hello my name is Alice.”将变成”olleH ym eman si ecilA.”

加解密算法

加解密的过程和哈希是不同的，它在计算的过程中需要提供一种称为密钥的参数：

加密算法(报文, 加密密钥) = 密文

解密算法(密文, 解密密钥) = 报文

如果加密密钥 == 解密密钥，则称为对称加密算法

如果加密密钥 != 解密密钥，则称为非对称加密算法

此外，根据加密计算的规则不同，还可以分为流加密算法和块加密算法 block

对称加密算法

对称密钥加密（Symmetric-key algorithm）又称为对称加密、私钥加密、共享密钥加密，是密码学中的一类加密算法。这类算法在加密和解密时使用相同的密钥，或是使用两个可以简单地相互推算的密钥。
常见的对称加密算法有XOR、DES、3DES、AES、Blowfish、IDEA、RC4等。

我们可以看下 openssl 命令下支持的对称加密方式

Base64

Base64编码在 web 编程中比较常用，可以简单的加密和解密，对安全性要求不高的可以使用。该加密算法不需要密钥。

import (
	"encoding/base64"
)
func base64Encode(src []byte) []byte {
	return []byte(base64.StdEncoding.EncodeToString(src))
}

func base64Decode(src []byte) ([]byte, error) {
	return base64.StdEncoding.DecodeString(string(src))
}

XOR 异或算法

异或算法是一种非常简单高效的算法。

XOR运算的定义是：两个值相同时，返回false，否则返回true。也就是说，XOR可以用来判断两个值是否不同。它还有个奇妙的特性：如果对一个值连续做两次 XOR，则会返回该值本身。

// 第一次 XOR
1010 ^ 1111 // 0101

// 第二次 XOR
0101 ^ 1111 // 1010

这个特性可以用户信息的加解密：

1 2	cipherText = message XOR key //加密 message = cipherText XOR key //解密

从上面的公式我们可以看出：

异或加密使用的加密密钥和解密密钥都是同一个，因此它属于对称加密算法。
由于异或加密是对信息的每个字节逐个比特进行异或运算，因此它属于流加密算法。
异或加密是通过比特位一个个的进行异或运算来进行的，对于密钥key 的长度有一定的要求。如果密钥 key 比信息 message 短，则 key 高位需要补齐0，这会导致 message 的高位与0异或后没有发生改变，也就是说多出来的部分没有被加密。因此要保证异或加密的安全性，密钥 key 必须长于要加密的信息，这限制了异或加密的使用场景。

AES 算法

AES 高级解密算法，是当年美国联邦政府采用的加密标准，其本质算法名称叫Rijndael加密算法，被 AES 标准采用。这个标准用来替代原先的DES算法，已经被多方分析且广为全世界所使用。

AES 算法基于排列和置换运算。排列是对数据位置重排，置换是将一个数据单元替换为另一个。AES 使用几种不同的方法来执行排列和置换运算。它可以使用128、192 和 256 位密钥，并且用 128 位（16字节）分组加密和解密数据。迭代加密使用一个循环结构，在该循环中重复置换和替换输入数据。

下面我们看看 golang 中的 AES 包的使用。

1	func NewCipher(key []byte) (cipher.Block, error)

该函数返回称为 Block 的结构(可以看出 AES 是块加密算法)，key 可以是16字节、24字节、32字节，分别对应了 AES-128、AES-192、AES-256。Block 的结构如下

type Block interface {
        // BlockSize returns the cipher's block size.
        BlockSize() int

        // Encrypt encrypts the first block in src into dst.
        // Dst and src must overlap entirely or not at all.
        Encrypt(dst, src []byte)

        // Decrypt decrypts the first block in src into dst.
        // Dst and src must overlap entirely or not at all.
        Decrypt(dst, src []byte)
}

从注释可以看到，这个结构只能加密或者解密数据的第一个块，因此对于数据长度大于block size 的情况，还需要进一步处理。这里引入密码学中的块密码的工作模式(mode of operation)的概念，它是指使用同一个密钥对多于一块的数据进行加密，并保证其安全性；它描述了加密每一数据块的过程，并常常使用基于一个通常称为初始化向量(IV)的附加输入值以进行随机化，以保证安全。常见的模式有ECB，CBC，OFB，CFB，CTR和XTS等。

我们以常见的 CBC 和 CFB 模式为例来看看如何使用。

import (
	"bytes"
	"crypto/cipher"
	"crypto/aes"
	"crypto/rand"
	"fmt"
)

//CBC 需要补齐不足的块
func AesCBCEncrypt(text, key []byte) ([]byte, error) {
	block, err := aes.NewCipher(key)
	if err != nil {
		return nil, err
	}
	text = PKCS5Padding(text, aes.BlockSize)
	// text = ZeroPadding(text, aes.BlockSize)
	
	// The IV needs to be unique, but not secure. Therefore it's common to
	// include it at the beginning of the ciphertext.
	ciphertext := make([]byte, aes.BlockSize + len(text))
	iv := ciphertext[:aes.BlockSize]
	//生成随机 iv 值
	if _, err := io.ReadFull(rand.Reader, iv); err != nil {
		panic(err)
	}
	
	mode := cipher.NewCBCEncrypter(block, iv)
	mode.CryptBlocks(ciphertext[aes.BlockSize:], text)
	//iv 和加密后的密文一起返回
	return cipherText, nil
}

//CBC 需要补齐不足的块
func AesCBCDecrypt(cipherText, key []byte) ([]byte, error) {
	block, err := aes.NewCipher(key)
	if err != nil {
		return nil, err
	}
	if len(cipherText) < aes.BlockSize {
        panic("ciphterText too short")
	}
	//密文前一部分为初始化向量 iv，无需保密
	iv := cipherText[:aes.BlockSize]
	cipherText = cipherText[aes.BlockSize:]
	
	// CBC mode always works in whole blocks.
	if len(cipherText) % aes.BlockSize != 0 {
		panic("cipherText is not a multiple of the block size")
	}
	
	mode := cipher.NewCBCDecrypter(block, iv)
	// CryptBlocks can work in-place if the two arguments are the same.
    mode.CryptBlocks(cipherText, cipherText)
	cipherText = PKCS5UnPadding(cipherText)
	// cipherText = ZeroUnPadding(cipherText)
	return cipherText, nil
}

func ZeroPadding(ciphertext []byte, blockSize int) []byte {
	padding := blockSize - len(ciphertext)%blockSize
	padtext := bytes.Repeat([]byte{0}, padding)
	return append(ciphertext, padtext...)
}

func ZeroUnPadding(origData []byte) []byte {
	length := len(origData)
	unpadding := int(origData[length-1])
	return origData[:(length - unpadding)]
}

func PKCS5Padding(ciphertext []byte, blockSize int) []byte {
	padding := blockSize - len(ciphertext)%blockSize
	padtext := bytes.Repeat([]byte{byte(padding)}, padding)
	return append(ciphertext, padtext...)
}

func PKCS5UnPadding(origData []byte) []byte {
	length := len(origData)
	// 去掉最后一个字节 unpadding 次
	unpadding := int(origData[length-1])
	return origData[:(length - unpadding)]
}

import (
	"bytes"
	"crypto/cipher"
	"crypto/aes"
	"crypto/rand"
	"fmt"
)

func AesCFBEncrypt(text, key []byte) ([]byte, error) {
	block, err := aes.NewCipher(key)
	if err != nil {
		return nil, err
	}
	
	// The IV needs to be unique, but not secure. Therefore it's common to
	// include it at the beginning of the ciphertext.
	ciphertext := make([]byte, aes.BlockSize + len(text))
	iv := ciphertext[:aes.BlockSize]
	//生成随机 iv 值
	if _, err := io.ReadFull(rand.Reader, iv); err != nil {
		panic(err)
	}
	
	stream := cipher.NewCFBEncrypter(block, iv)
	stream.XORKeyStream(ciphertext[aes.BlockSize:], text)
	//iv 和加密后的密文一起返回
	return ciphertext, nil
}

func AesCFBDecrypt(cipherText, key []byte) ([]byte, error) {
	block, err := aes.NewCipher(key)
	if err != nil {
		return nil, err
	}
	if len(cipherText) < aes.BlockSize {
        panic("ciphterText too short")
	}
	//密文前一部分为初始化向量 iv，无需保密
	iv := cipherText[:aes.BlockSize]
	cipherText = cipherText[aes.BlockSize:]
	
	stream := cipher.NewCFBDecrypter(block, iv)

	// XORKeyStream can work in-place if the two arguments are the same.
	stream.XORKeyStream(cipherText, cipherText)
	return cipherText, nil
}

从上面代码可知，如果待加密的长度正好被整除，即不需要padding，实际处理时其实是做了全补足，否则是没法去去掉padding内容，因为补的长度被放置在最后一个字节，前面最少补1个字节，最多补blockSize个字节。

RC4算法

RC4（来自Rivest Cipher 4的缩写）是一种流加密算法，密钥长度可变。它加解密使用相同的密钥，因此也属于对称加密算法。 RC4是有线等效加密（WEP）中采用的加密算法，也曾经是TLS可采用的算法之一。

RC4算法的基本原理是先根据 key 和伪随机算法得到辅助加密用的和明文等长的 SBox，然后将 SBox 和明文进行逐字节异或XOR得来。由于RC4算法加密是采用的XOR，所以，一旦子密钥序列出现了重复，密文就有可能被破解。

目前 RC4算法已经被破解，不再推荐使用。

非对称加密算法

非对称加密算法使用两把完全不同但又是完全匹配的一对钥匙：公钥和私钥。在使用不对称加密算法时，只有使用匹配的一对公钥和私钥，才能完成对明文的加密和解密过程。这对于对称加密算法来说，又安全了一步。除了加解密之外，非对称算法还可以用于数字签名，数字签名是一种用于验证对方身份的技术。

具体使用时，遵循以下规则

加密应用，使用公钥加密，私钥解密
签名应用，使用私钥签名，公钥验证

下面介绍下常用的非对称加密算法。

RSA 算法

RSA算法基于大数因子分解难题，其核心问题是欧拉定理，是目前唯一被广泛接受并实现的通用公开加密算法。这种算法非常可靠，密钥越长，它就越难破解。根据已经披露的文献，目前被破解的最长RSA密钥是768个二进制位。也就是说，长度超过768位的密钥，还无法破解（至少没人公开宣布）。因此可以认为，1024位的RSA密钥基本安全，2048位的密钥极其安全。

RSA加密的大致流程是

乙方生成两把密钥（公钥和私钥）。公钥是公开的，任何人都可以获得，私钥则是保密的。
甲方获取乙方的公钥，然后用它对信息加密。
乙方得到加密后的信息，用私钥解密。

如果公钥加密的信息只有私钥解得开，那么只要私钥不泄漏，通信就是安全的。在实际使用中，一般选择 1024 位的密钥即可。

ECC 算法

ECC，全称 Elliptic-curve cryptography，基于解决椭圆曲线离散对数问题的困难性上。ECC 相对于其他非对称加密方式的主要优势是其密钥更小(最小密钥长度 RSA1024位，ECC 160位)，并且提供更高的安全性，但是其加解密花费的时间相对其他要长。

下面是基于 golang 官方 elliptic 库封装的 ECC 算法

type GoECDH struct {
    elliptic.Curve
}

func NewGoECDH(curve elliptic.Curve) *GoECDH {
    if curve == nil {
        curve = elliptic.P256()
    }
    return &GoECDH{
        Curve: curve,
    }
}

func (ge *GoECDH) GenerateKeys() (pub []byte, priv []byte, err error) {
    p, x, y, e := elliptic.GenerateKey(ge.Curve, rand.Reader)
    if e != nil {
        err = e
        return
    }
    pub = elliptic.Marshal(ge.Curve, x, y)
    priv = p
    return
}

func (ge *GoECDH) MakeSecret(pub []byte, priv []byte) []byte {
    x, y := elliptic.Unmarshal(ge.Curve, pub)
    secret, _ := ge.Curve.ScalarMult(x, y, priv)
    return secret.Bytes()
}

参考资料

维基百科经典密码

XOR 加密简介

golang中 AES 加密详解

密码学简介与Golang的加密库Crypto的使用

NAS设置公网访问

发表于 2018-07-27 |

引子

入手了群晖 NAS 之后，一直使用厂家提供的 quickconnect 来从外网访问家里的 NAS。quickconnect 的原理其实是要通过群晖的服务器进行中转，然后再连接 NAS，由于服务器不在国内，其传输速度可想而知，通常就是几十上百 K的水平。如果只是通过 web 连接 NAS 来管理或者操作FileStation 来下载还是勉强可用的，但是如果要从外网上传文件到 NAS 或者从 NAS 下载，这种速度是不可忍受的。

直连

要提高速度的办法，只能是外网直连 NAS 了。但是一般 NAS 都会部署在家里或者公司的内网环境，要能从外网访问，一般需要使用路由器带的端口转发或者 DMZ 功能。具体流程就是

外网通过公网 IP 连接到路由器
路由器通过端口转发，将特定端口的包转发给内网同一网段的 NAS，从而实现通信

不过，在开始前，我们还有几个问题需要预先解决

首先，国内大部分网络环境是光猫拨号进行上网，运营商默认会设置光猫为路由(Route)模式，猫自动进行 PPPoE拨号，同时也带有简单的路由功能，于是我们可以直接连接猫的 Lan 口进行上网。但是一般猫的路由功能很鸡肋，往往没有无线 Wifi 功能，带的 Lan 口也有限，所以一般会在猫后面接一个专用路由器来管理家里的诸多设备及无线上网。所以 NAS 是连接到路由器，再通过光猫连接到公网环境的。这带来一个问题：如果我们能连接到光猫，也没法直接访问内网的 NAS。所幸光猫还提供了一种成为桥接(Bridage)的模式，意思是将外网和光猫后面的设备(也就是我们的路由器)进行直连，由我们的路由器来进行拨号，而光猫本事是透明的，只是用来透传数据。

运营商一般会给用户默认分配内网 IP，这导致我们没法连接到家里的路由器。因此需要联系运营商，让他们分配公网 IP 给我们。

这些完成之后，我们就可以检查公网是否能访问自己的网络了，使用 ping 来检查是否畅通(如果有路由上设置了禁止 ping，需要关闭该设置)

1	$ ping xxx.xxx.xxx.xxx

这里xxx.xxx.xxx.xxx是运营商分配给你的公网 IP，你可以替换为自己的来进行测试。

有时候猫或者路由上设置了防火墙，禁止 ping，所以需要关闭该设置再进行测试。

一般 NAS 服务的访问端口是5000(http)和5001(https)，这个可以在 NAS 里进行设置：

假如 NAS 的内网 ip 是10.0.0.11，那在内网可以通过10.0.0.11:5000来访问。现在如果想在外网访问 NAS，比如说是通过 http://xxx.xxx.xxx.xxx:5000 ，那么我们就需要在路由器上配置端口转发，将路由器上所有对5000端口的访问都转发到内网 NAS 地址(即10.0.0.11)的5000端口。各个路由器可能不一样，我们这里以 R7000的梅林系统为例：

设置完成后，我们测试一下端口是否可以正常访问

至此，通过公网 IP 我们已经顺利访问了 NAS，就如同内网访问一样。

域名访问

到目前为止，似乎一切都很美好。但是需要提出的是，运营商分配分配给我们的公网 IP 往往是动态变化的，并不固定，所以如果 IP 不停发生着变化，在访问 NAS 之前我们就必须查询一次自己的 IP。好在有种称为 DDNS 的技术，可以解决这个问题。

DDNS(Dynamic Domain Name Server) 翻译过来是动态域名服务，也就是不管我们的 IP 怎么动态变化，域名都能准确指向它，因此通过这个动态域名，我们就无需关心实际的 ip 是什么，每次都能访问到 NAS 上。

很多路由器都带有 DDNS 功能，其工作原理大致是每次 ip 发生变化时，路由器都会将当前的 ip 上报更新到 DDNS 服务提供商，因此域名解析出来的 ip 也会随之得到更新。

假设我们在路由器上开启 DDNS 时设置的域名是 myddns.asuscomm.com

那么之后我们就可以通过 myddns.asuscomm.comm:5000来访问了。如果你有自己的域名，则可以设置一个 cname 类型的域名来指向 myddns.asuscomm.comm 域名。

如果路由不带 DDNS 功能，可以考虑使用 NAS 的 DDNS 功能(有很多提供商可以选择)，具体请 google 设置方法。国内花生壳也提供了 DDNS 功能。

参考资料

将群晖 NAS 安全地暴露到公网中

philipyao

GitHub E-Mail