游戏服务器是一种很常见的分布式系统,分布式系统最大的难题是状态同步,CAP 定理是这方面的原理。
CAP定理
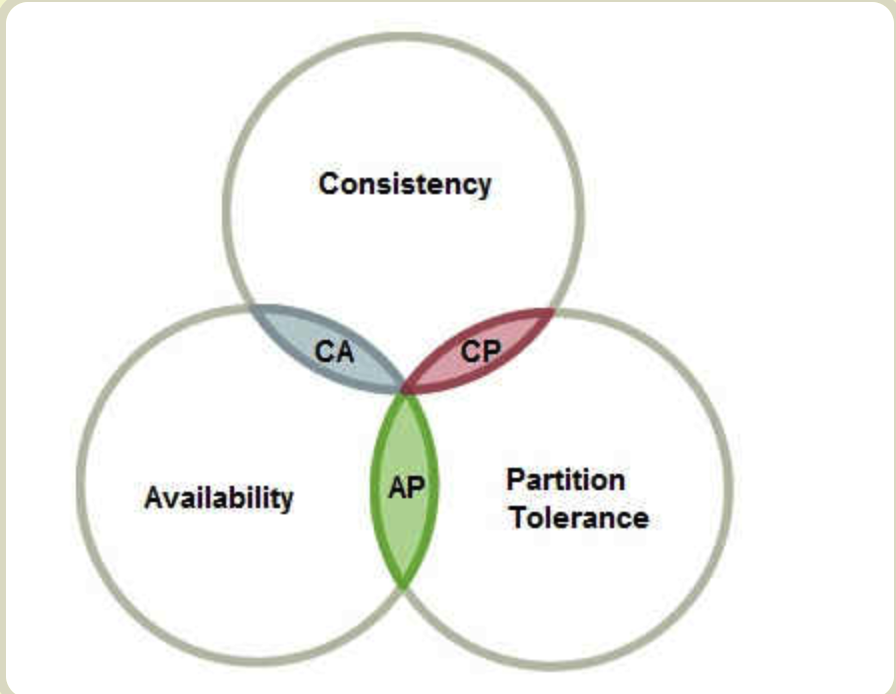
Consistency 一致性
Availability 可用性
Partition tolerance 分区容错性
CAP 这三个指标不可能同时做到,最多只能满足其二。这个结论就叫做 CAP 定理。
Partition tolerance 分区容错,意思是分布式的各节点(也叫区)之间通信是不可靠的。一般来说,分区容错无法避免,因此可以认为 CAP 的 P 总是成立。CAP 定理告诉我们,剩下的 C 和 A 无法同时做到。
Consistency 一致性,意思是从各个节点访问同一数据,其值必须都是最新的,即一致的。节点的多份数据必须通过一定的算法做同步。
举例来说,某条记录是 v0,用户向 G1 发起一个写操作,将其改为 v1。
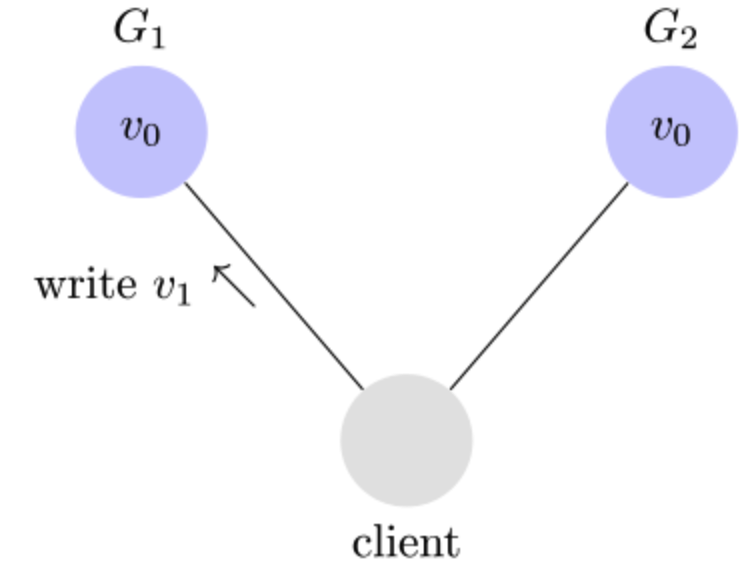
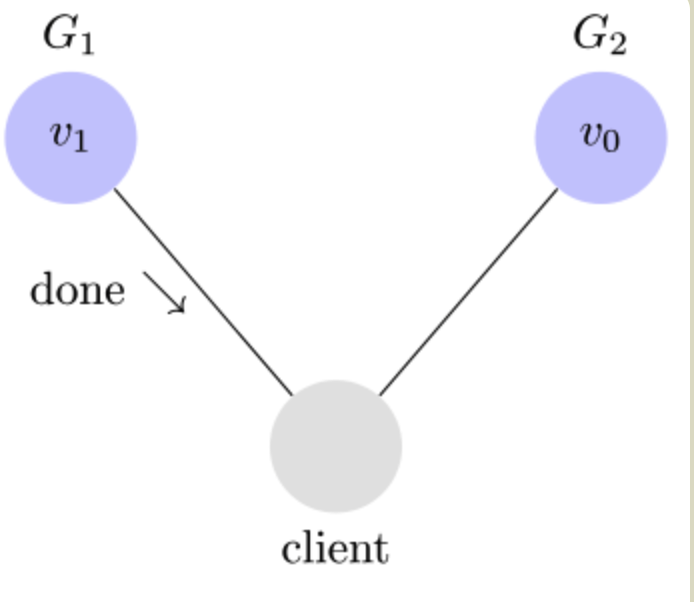
此时如果有用户向 G2 发起读操作,由于 G2 的值没有发生变化,因此返回的是 v0。G1 和 G2 读操作的结果不一致,这就不满足一致性了。
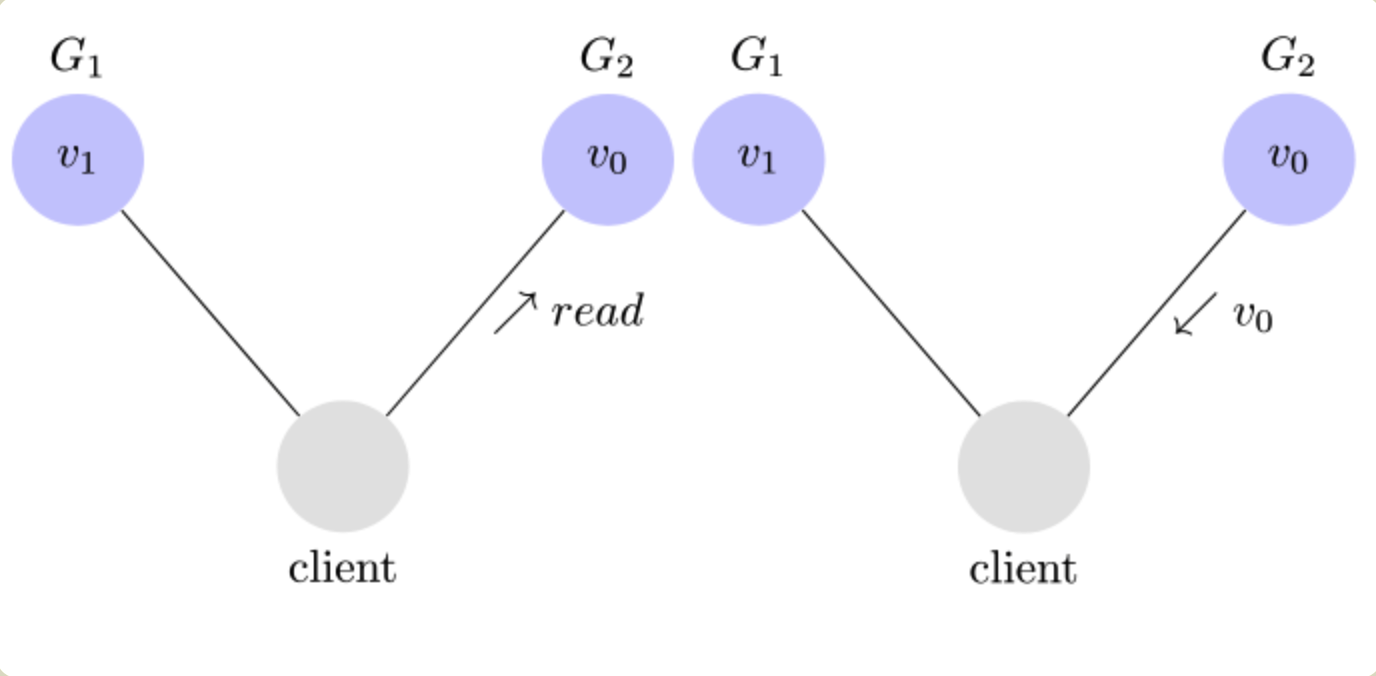
为了让 G2 也能变为 v1,就要在 G1 写操作的时候,让 G1 向 G2 发送一条消息,要求 G2 也改成 v1。
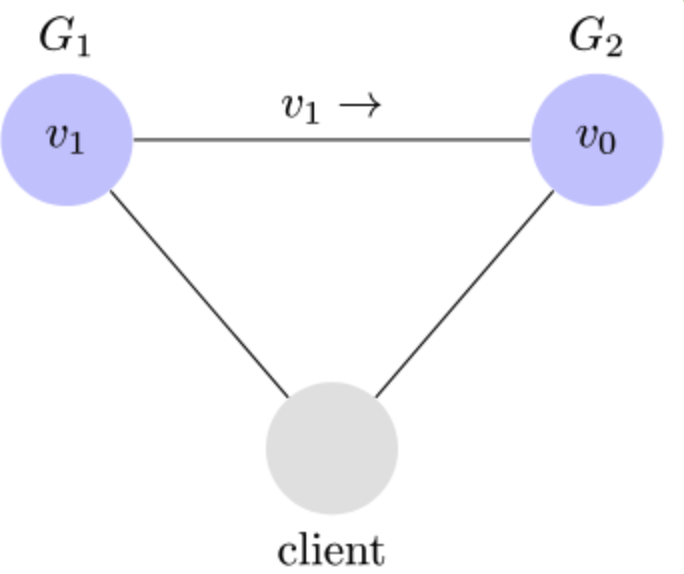
注意这里说的其实是强一致性。相对的还有弱一致性,即最终一致性。
Availability 可用性, 意思是通过任意节点都可以拿到数据,强调服务的可用性。一般可以用 服务可用时间/总服务时间 去度量。比如4个9的可用性,即99.99%,换算到一年的时间内,可以反推出最长故障时间:
365 × 86400 ×(1-99.99%)秒 = 3153.6 秒 = 52.56 分钟
保证系统各个环节无单点、大部分故障可自愈是保障高可用性的关键。
以下为一些案例:
- CDN 缓存。最大可用性 + 最终一致性。各CDN节点的数据可以在运行一段时间后才趋于一致。
- zookeeper。强一致性 + 不错的可用性。paxos/raft 一致性算法保证一致性。当出现分区(P故障)的时候,并非是完全不可用的,它提供了在大多数节点连通的情况下的可用性保证。
- 两阶段提交协议:强一致性 + 糟糕的可用性。两阶段提交协议中任意一节点与协调节点之间发生了分区,则服务完全终止。
- Git。优先保证可用性,一般就是提交在本地。远程合并时,有一个专门的合并算法处理一致性问题,遇到无法处理的冲突(小部分情况下),把选择权交给了用户。
游戏中的数据一致性
游戏是一种逻辑极其复杂,数据结构繁杂的系统,需要处理的问题千差万别;不同的游戏类型,其要求也是不同的,不能简单的套用理论上的CAP定理,去过分强调系统的一致性或者可用性。对于游戏中产生的数据,我们可以分为以下几大类:
- 玩家的存档数据。这部分数据可以说是游戏中最重要的数据了,通常我们的考虑是强一致性。
- 全局重要数据,如工会数据、SLG大地图城池数据等。这也要求强一致性。
- 旁路数据,如好友列表数据。因为好友信息,如名字、等级、头像等,这些数据的更新有一定的延迟容忍度,可以做成弱一致性,保证最终的数据一致性即可。
多方修改
对于玩家存档数据和全局重要数据,很可能有多方同时修改,如何保证强一致性呢?
方法一,某一玩家的数据读取或者修改统一指定到特定逻辑进程来操作。例如A在进程1,玩家B在进程2,如果A想读取或者修改B的数据,将修改请求统一发放到进程2处理,完成后返回进程1。这样处理有个问题,如果某一个进程挂掉,该进程上的玩家都无法得到服务。好处是简单,没有同时读写的问题。
方法二,所有进程对等,玩家操作不一定落在某一固定进程处理,所有进程的需要做的就是取玩家的数据,修改,然后存入数据层。一般在逻辑层做乐观锁机制,保证多进程同时修改一个玩家数据。简单的可以设置一个版本号,更新的时候去检查版本号,不一致则失败,需要做回滚。这种情况一般要求业务需求可以重试,如很多游戏里的偷菜等玩法就采用这种方式。复杂的地方在回滚怎么做。这种方式的并发性能比较高。
方法三,对于同时操作概率比较大的数据,如公会数据、大地图数据等,可以添加独占锁,严格保证一致性。这种方式性能会比较低,并发不高。可以做的改进是用读写锁。
方法二和方法三的情况,无论是操作玩家数据或者全局数据,本质上都是用的是锁(乐观锁和悲观锁),所以要注意尽量减小锁的粒度,做垂直划分:将关联度低的数据拆分成多块,分别加锁控制,减小锁冲突。
数据软拷贝
所谓数据软拷贝,意思是对核心数据的冗余备份,用以提高性能和逻辑复杂度。
举个例子,上文提到的好友列表中的某一个玩家的数据,如名字、等级等,在该玩家存档数据中一定是准确的,这个由强一致性保证。这是不是意味着拥有该玩家为好友的所有其他玩家,其好友列表中一定要实时更新?答案是否。我们可以为所有玩家维护一份冗余的简要数据放到全局服务中;各逻辑服如果有玩家存档数据更新,只需要同时通知简要数据修改,但可能更新失败,这可以容忍。下次找个时机,如玩家登录时再使用存档数据同步一下简要数据。拉取玩家好友列表,直接取简要数据里的数据即可。
另一个例子,是公会相关数据。全局的公会数据需要维护公会的基本信息,以及成员的信息;同时玩家存档数据需要记录自己属于哪个公会。这里我们就需要区分数据准确性,通常认为公会数据是准确的,玩家存档里的是软拷贝。如果有一个玩家加入公会,永远以公会数据做基本判断,加入成功后再同步玩家存档数据。如果同步出错怎么办?其实问题不大,只是其他玩家看到的软拷贝是脏数据。找个时机,如玩家登录时从公会服拉取同步一下,或者公会服控制定时 push 到游戏逻辑服。
事务数据
分布式事务经常出现在互联网产品中,如电商后台的订单系统,就会涉及一个操作修改多份数据:下单会修改商品库存、订单、支付信息等,要求事务性。
游戏中类似的系统有建角,双向好友,拍卖行,特定玩法如俘虏与被俘虏等。
一种做法是用状态机,将事务的各个操作拆分N个原子操作,然后每一步都有其对应的回滚逻辑,如果中间失败,依次回滚。
另一种做法是互联网产品中经常使用的方式,利用消息队列的方式保存消息,利用消息队列的重传特性,如果中间失败,则会重传继续重试。这里要注意,对于操作要做到幂等性,即使重试多次调用接口不会多次运行逻辑。
不使用两阶段提交是因为,有可能多个原子步骤之间有依赖关系;并且两阶段提交整个过程是阻塞的,第一阶段prepare 会锁住资源,这是不可接受的。
参考资料