定时器实现

定时器是游戏开发中常用的基础组件，本文介绍几种定时器组件的实现方法。

Linux 内核定时器实现

Linux 内核的定时器从1997年之后基本没有修改过，最终版本是使用时间轮算法的定时器。定时器的最大设置超时范围是 2^32 个jiffies。设置 jiffie 为毫秒级或者秒级，就可以控制定时器的精度。例如 jiffie 设置为100ms，即1秒相当于10个jiffie，则定时器的最大范围是

2^32 / 10 / 86400 = 4971 天

该实现主要提供了以下接口添加或者删除定时器：

timer = add_timer(expire)
del_timer(timer)

定时器的超时 expire 被定义位 n 个 jiffies

如果定时器超时，则调用注册的回调函数

timer->fn(timer->data)

最初始定时器的实现采用的是最简单的方式，就是将所有的定时器串成一个有序的双向链表。

这种方式添加定时器的方式就是从前往后遍历顺序链表，找到合适的位置插入，时间复杂度是 o(n)；删除定时器则非常简单，是 o(1)复杂度；超时复杂度也是 o(1)。这种定时器的实现方式缺点在与管理大量定时器时，效率不高。

另一种能想到的定时器实现方式，是使用二叉排序树。左子树的超时时间比右子树的超时时间小，于是每次添加定时器时只需要二分查找，因此复杂度是 o(log(N))；删除和超时则是 o(1)；

还有一种方式，就是申请 2^32个桶，然后每个桶中维护一个 list 用来存放定时器，而每个 jiffie 对应一个桶，定时器的插入操作就是简单的索引到桶，然后执行 list_add() 操作，时间复杂度变为 o(1)；同样的，删除和超时都是 o(1) 操作。其实这就是最初版本的基于时间轮的算法，如下图所示

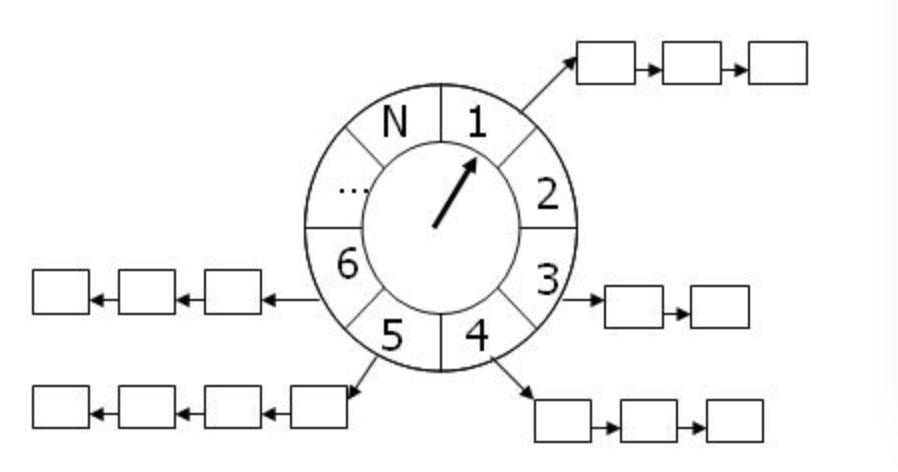
这种方式时间复杂度是最低的，但是其需要的内存空间巨大，尤其是在定时器数量不多的时候，是个很大的浪费。

那么，有没有一种方式是对这种桶方式的改进，能同时满足时间复杂度和空间复杂度呢？这就是目前采用的多精度时间轮算法。多精度有种很形象的比喻，就是平时看到的水表

在上面的水表中，为了表示度量范围，分成了不同的单位，比如 1000，100，10 等等，相似的，表示一个 32bits 的范围，也不需要 2^32 个元素的数组。

具体实施时，将所有的 jiffie 分成5组：

1..256, 257..16384, 16385..1048576, 1048577..67108864, 67108865..4294967295

第一组，就是即将到期的256个jiffie，为每个 jiffie 分配一个桶(bucket)，一共是256个桶。 这里每个桶里定时器的到期时间都是相同的，精度为1jiffie。

第二组，我们分为64个桶，每个桶里存放接下来到期的256个 jiffie 对应的定时器。在这里，可以看到桶里定时器的到期时间是不同的，也就是精度是256 jiffies。

第三组，还是分为64个桶，于是每个桶的精度就是 256 * 64 = 16384 jiffies。

第四组，还是分为64个桶，每个桶的精度是 256 64 64 = 1048576 jiffies。

最后一组，依旧分为64个桶，每个桶的精度是 256 64 64 * 64 = 67108864 jiffies。

最终我们用到的桶的数量是 256+64+64+64+64 = 512 buckets。也就是说我们通过控制桶的精度，将2^32个 jiffies (32 bits) 分成了 8 + 6 + 6 + 6 + 6 bits 。可能有人问了，为什么这么分呢，为什么不是 8 + 8 + 8 + 8 ? 从作者的回复来看，主要是 256 + 256 + 256 + 256 = 1024个桶，这比512个桶空间占用多。

那么如何插入定时器呢？首先根据定时器的 expire 来定位到放到哪一组中，然后再定位到具体的桶 index。注意，除了第一组之外其他组的桶中，定时器的到期时间都可能是不同的。例如到期时间分别是 260 jiffies 和 265 jiffies 的定时器都会被放入第二组的第一个桶中( 257 jiffies ~ 512jiffies 都在这个桶中)。这表示这些桶中的定时器是『部分排序的』，本质上是对他们的高位进行排序。插入定时器的操作只是定位到具体的桶 index，然后执行 list_add() 操作(链表本身不需要排序)，时间复杂度是 o(1)；而删除也是一样定位组和桶 index，时间复杂度 o(1)。

问题是怎么执行定时器的超时呢？第一组里的256个桶没有问题，我们只需要在时间轮的指针逐次增加1并指向对应的 jiffies 时，执行其对应桶里的所有定时器即可。那如果指针指向第 257 jiffie 呢？从前面的分析我们可以知道，第 257 jiffie 指向的桶里可能包含 257 jiffies ~ 512 jiffies 这 256个 jiffies 的定时器，它们是非顺序地存储在桶的链表内，不能直接执行。执行前，需要做的就是将这个桶里的所有定时器全部重新映射到第一组的256个桶里，即将粗精度的定时器重新进行细精度的划分/排序。由于时间指针已经指向第257 jiffies，那么第二组第一个桶里的所有定时器的相对超时时间必定都减少了256 jiffies，因为重新添加时，会落到第一组的细精度桶区间内。同样的过程，我们在指针指向第三组 (16385jiffies ~ 1048576jiffies) 的定时器时，将这组里各桶的定时器重新添加映射到前面两组的桶内。后面各组的执行也类似。

重新添加/映射完成之后，每次我们只用执行相对于定时器指针相差 256个 jiffies 的定时器(也就是总是执行第一组里的定时器)，如果超过256则再继续执行重新添加/映射，再执行映射后的第一组，如此循环。

本质上，这种策略称为一种『延迟排序』，即定时器在很久到期时，我们对其进行粗粒度的排序，即只排序高位，就是定位放入哪个桶即可，从而提高效率。而当快要执行时，才将其进行细粒度排序及定位。这带来一个很明显的好处是，如果定时器不执行(即到期前就被删除)，由于添加和删除的时间复杂度都是 o(1)，其效率将非常高。

在定时器的实际使用时，很多确实是没有到期即被删除。可以想像下大量防止网络超时的定时器。

最小堆定时器

最小堆也是实现定时器的一种常用方式，例如 libevent 库的定时器就是使用的最小堆优先级队列。Golang 官方库中的 timer 也是使用的最小堆原理。

所谓最小堆，其实是一颗特殊的二叉树，其所有节点的值都比左右子节点的值要小。因此整个二叉树的最小值就在 root 元素。每次检查定时器是否到期时，我们检查 root 元素是否到期即可。同时，这棵二叉树又是一个完全二叉树。如果一棵二叉树除了最右边位置上一个或者几个叶结点缺少外其它是填满的，那么这样的二叉树就是完全二叉树。严格的定义是：若设二叉树的高度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层从右向左连续缺若干结点，就是完全二叉树。下面这几颗二叉树都是完全二叉树

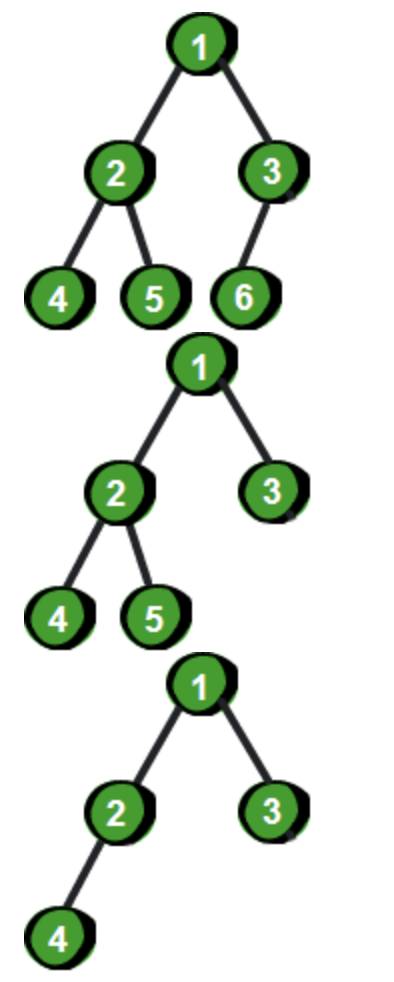
其基本类似于下面这个形状：

那如何表示一颗完全二叉树呢？只需要一个数组即可。首先将完全二叉树进行从上到下，从左到右编号：

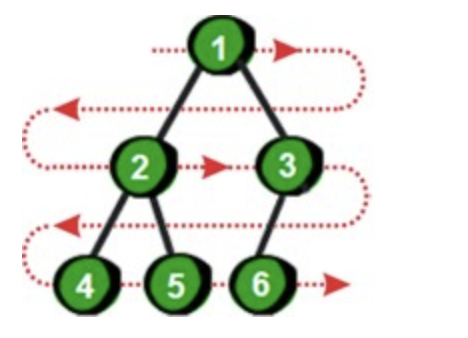
通过上图我们发现如果完全二叉树的一个父结点编号为 k，那么它左儿子的编号就是 2k，右儿子的编号就是 2k+1。如果已知儿子（左儿子或右儿子）的编号是 x，那么它父结点的编号就是 x/2，注意这里只取商的整数部分。在 C 语言中如果除号‘/’两边都是整数的话，那么商也只有整数部分（即自动向下取整），即 4/2 和 5/2 都是 2。另外如果一棵完全二叉树有 N 个结点，那么这个完全二叉树的高度为 log2 N 简写为 log N，即最多有 log N 层结点。

如果我们现在想添加一个定时器，也就是新增一个节点(例如值为3)，该如何操作呢？只需要直接将新元素插入到末尾，再根据情况判断新元素是否需要上移，直到满足堆的特性为止。如果堆的大小为 N（即有 N 个元素），那么插入一个新元素所需要的时间也是 O(logN)。

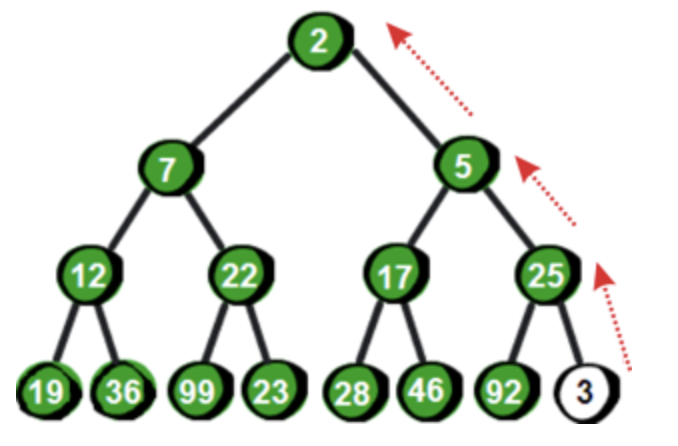
先将 3 与它的父结点 25 比较，发现比父结点小，为了维护最小堆的特性，需要与父结点的值进行交换。交换之后发现还是要比它此时的父结点 5 小，因此需要再次与父结点交换。至此又重新满足了最小堆的特性。

向上调整的代码如下

void siftup(int i) //传入一个需要向上调整的结点编号i
{
    int flag=0; //用来标记是否需要继续向上调整
    if(i==1)  return; //如果是堆顶，就返回，不需要调整了    
    //不在堆顶 并且 当前结点i的值比父结点小的时候继续向上调整 
    while(i!=1 && flag==0)
    {
        //判断是否比父结点的小 
        if(h[i]<h[i/2])
            swap(i,i/2);//交换他和他爸爸的位置 
        else
            flag=1;//表示已经不需要调整了，当前结点的值比父结点的值要大 
        i=i/2; //这句话很重要，更新编号i为它父结点的编号，从而便于下一次继续向上调整 
    }
}

定时器到期又是如何处理呢？根据最小堆的特性，先到期的就是 root 节点，因此执行定时器函数后，我们将 root 元素删除，同时将堆的最后一个节点移动到 root 位置，然后看是不是需要执行向下调整，以保持最小堆的特性。

向下调整的代码如下

void siftdown(int i) //传入一个需要向下调整的结点编号i，这里传入1，即从堆的顶点开始向下调整 
{
    int t,flag=0;//flag用来标记是否需要继续向下调整 
    //当i结点有儿子的时候（其实是至少有左儿子的情况下）并且有需要继续调整的时候循环窒执行
    while( i*2<=n && flag==0 )
    {        
        //首先判断他和他左儿子的关系，并用t记录值较小的结点编号 
        if( h[i] > h[i*2] )
            t=i*2;
        else
            t=i; 
        //如果他有右儿子的情况下，再对右儿子进行讨论 
        if(i*2+1 <= n)
        {
            //如果右儿子的值更小，更新较小的结点编号  
            if(h[t] > h[i*2+1])
                t=i*2+1;
        }
        //如果发现最小的结点编号不是自己，说明子结点中有比父结点更小的  
        if(t!=i)
        {
            swap(t,i);//交换它们，注意swap函数需要自己来写
            i=t;//更新i为刚才与它交换的儿子结点的编号，便于接下来继续向下调整 
        }
        else
            flag=1;//则否说明当前的父结点已经比两个子结点都要小了，不需要在进行调整了 
    }
}

同样的，如果要在定时器到期之前删除它，就类似于删除最小堆的任一节点。方式是将最后一个节点放置到该删除的节点，然后从该节点开始执行向下调整，直到整个堆又满足最小堆的特性，本质上和定时器到期时删除 root 节点的思路是一致的。时间复杂度也是 O(logN)。

参考资料

Linux 下定时器的实现方式分析

kernel timer design

极客时间：二叉树