游戏中的加密应用

发表于 |

游戏中加密算法的选择

前面一篇文章 我们已经介绍了对称解密算法和非对称加密算法，那在游戏协议通信中应该如何选择加密方式呢？

那我们看看下列几个方案

  1. 单独使用对称加密算法。典型的对称加密算法如 AES 安全性已经不错，而且加密效率高，似乎可以直接拿来使用。但问题是客户端和服务器交互时如何交换密钥？如果直接明文传输，肯定会有被嗅探的风险。所以单独使用对称加密算法存在密钥的管理问题，是不可行的。
  2. 单独使用非对称加密算法。非对称加密算法基于未解决的数学难题，因此在破解上几乎不可能。其优点就是安全，但缺点就是不够快，比较耗费cpu，如果在游戏中每一次消息都用其加密，对cpu的损耗还是挺高的。

一种折中的办法是：采用密钥交换算法交换对称加密算法的密钥，然后用对称加密算法加密数据。

所谓密钥交换，通俗地说，即使有攻击者在偷窥你与服务器的网络传输，客户端（client）依然可以利用“密钥协商机制”与服务器端（server）协商出一个用来加密应用层数据的密钥（也称“会话密钥”）。

那么如何进行安全的密钥交换呢？

  • 一种方案是使用非对称加密算法。原理是通信一方首先生成密钥对，私钥自己保存，然后将公钥发送给另外一方；另一方拿到公钥后，随机生成一个对称加密的密钥，然后利用公钥加密它；再把加密结果发给对方，对方用私钥解密；于是双方都得到了会话密钥。 后续通信就使用该密钥进行对称加解密。例如早期的 SSLv2只支持一种密钥协商方式，就是 基于RSA 非对称加密算法的密钥协商机制。

  • 第二种方案是使用专用的密钥交换算法，如 DH算法及其改进型 ECDH算法。该交换算法比较复杂，我们在后面的内容中进行介绍。

  • 还有一种方案就是基于 PSK的密钥协商。PSK 全称Pre-Shared Key，顾名思义，就是预先让通讯双方共享一些密钥（通常是对称加密的密钥）。所谓的预先，就是说，这些密钥在 TLS 连接尚未建立之前，就已经部署在通讯双方的系统内了。其具体步骤是在通讯之前，通讯双方已经预先部署了若干个共享的密钥。为了标识多个密钥，给每一个密钥定义一个唯一的 ID。协商的过程很简单：客户端把自己选好的密钥的 ID 告诉服务端。如果服务端在自己的密钥池子中找到这个 ID，就用对应的密钥与客户端通讯；否则就报错并中断连接。

最后一种方式考虑到所有会话都使用这些固定的密钥，比较少用到。我们只看前两种方式。

DH 系交换算法

DH 算法

DH，全称Diffie–Hellman key exchange，是一种安全协议。它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥。这个密钥可以在后续的通讯中作为对称密钥(通过对称加密算法)来加密通讯内容。

其基本原理如下

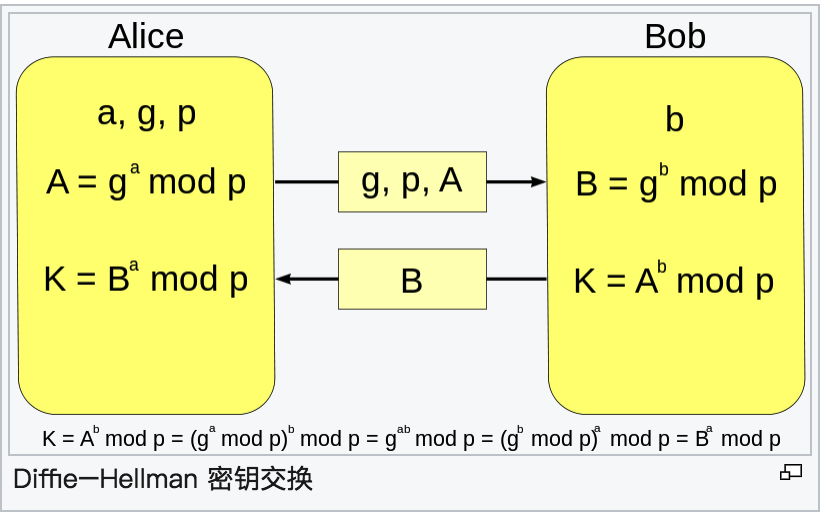
image-20180801200114787

如果 p 是一个至少 300 位的质数，并且a和b至少有100位长， 那么即使使用全人类所有的计算资源和当今最好的算法也不可能从g, p和ga mod p 中计算出 a。这个问题就是著名的离散对数问题。注意g则不需要很大, 并且在一般的实践中通常是2或者5。

密钥交换的流程主要有2步：

  1. 初始化密钥对，并向对方公布自己的公钥
  2. 构建本地密钥，作为后续加密的密钥

以消息传递模型为例，甲方为发送者，乙方为接收者，分述甲乙双方如何构建密钥，交换密钥和加密数据。

首先，甲乙双方需要在收发信息前构建自己的密钥对，如下图：

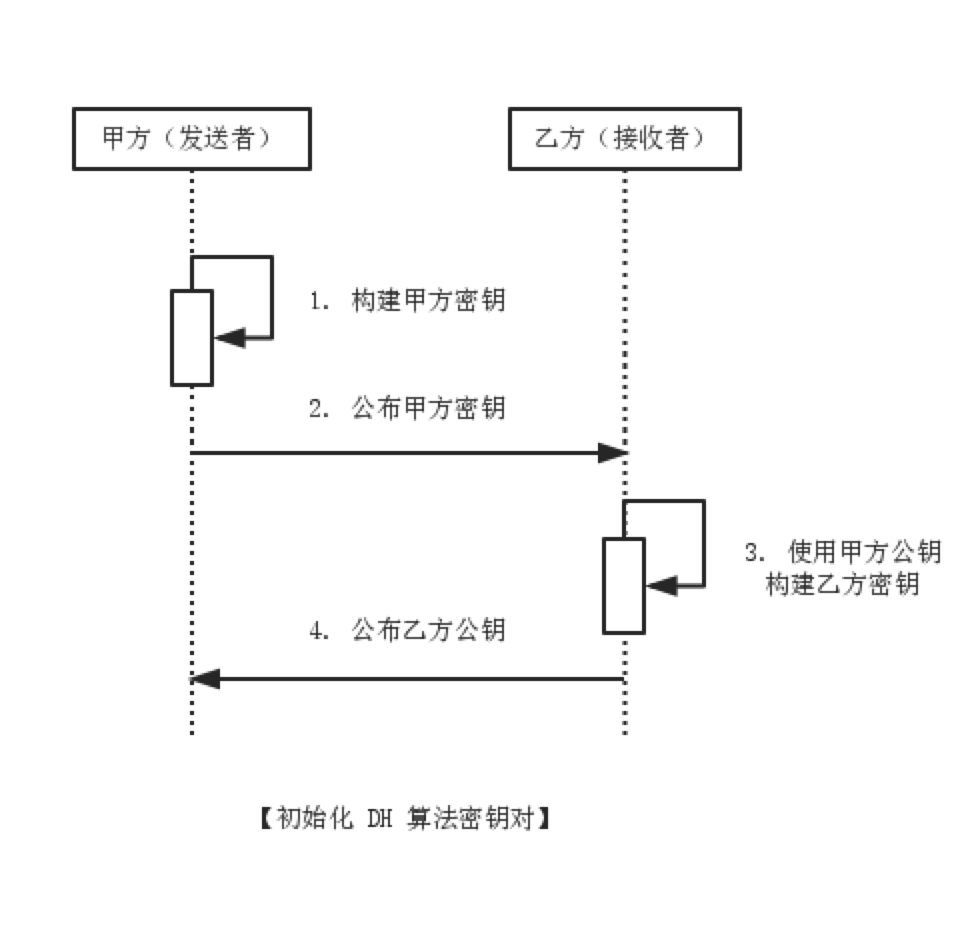
image-20180801194410265

注意，乙方构建自己的密钥对必须使用甲方公钥作为参数，否则无法确保甲乙双方获得同一个私密密钥，消息加密更无从谈起。 其次，假设甲乙双方事先约定好了用于数据加密的对称加密算法（如 AES 算法），并构建本地密钥（即对称加密算法中的密钥）， 甲方需要使用自己的私钥和乙方的公钥才能构建本地密钥，即用于数据加解密操作的对称加密算法密钥。 同样，乙方需要使用自己的私钥和甲方的公钥构建本地密钥。如下图：

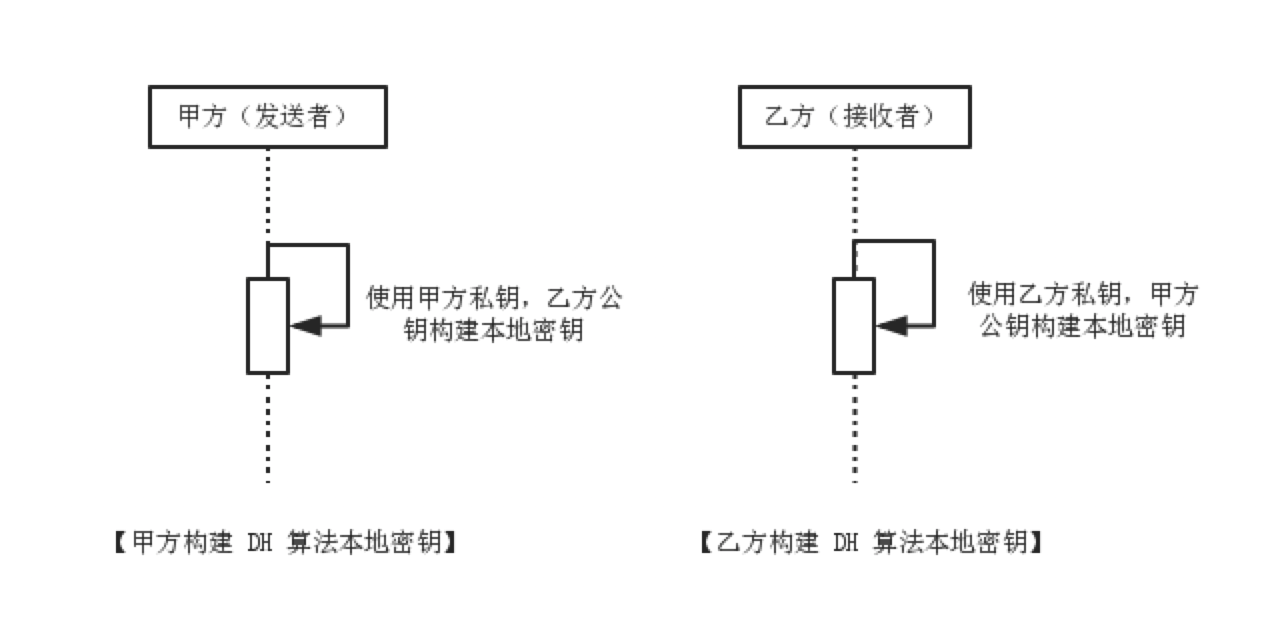
image-20180801194540530

虽然甲乙双方使用了不同的密钥来构建本地密钥，但得到的密钥是一致的，正因为如此，甲乙双方才能顺利进行加密消息的传递。 最后，甲乙双方构建了本地密钥后，可按基于对称加密算法的消息传递模型完成消息传递，如下图：

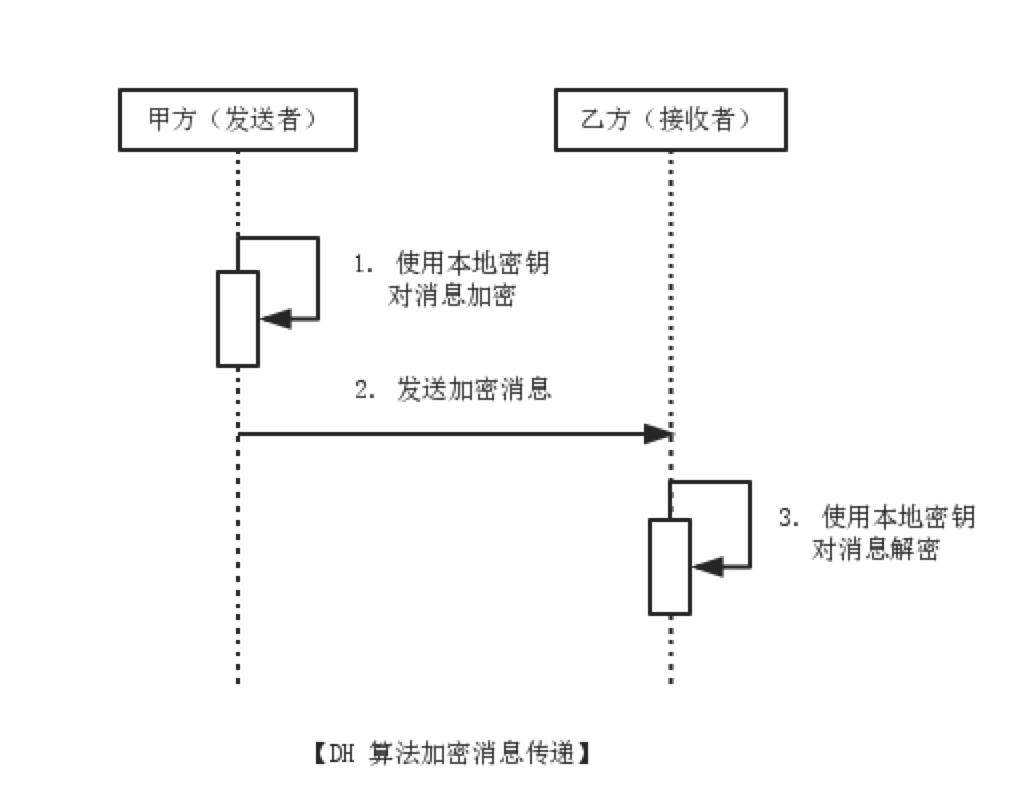
image-20180801201756669

ECDH算法

DH 算法有一个变种，称之为 ECDH（全称是“Elliptic Curve Diffie-Hellman”）。

它与 DH 类似，差别在于： DH 依赖的是——求解“离散对数问题”的难题。 ECDH 依赖的是——求解“椭圆曲线离散对数问题”的难题。其密钥交换过程于 DH 算法基本一致，这里我们不在赘述。

PFS 特性的保证

PFS 全称perfect forward secrecy，中文翻译叫『完美前向保密』，是由Christoph G. Günther在EUROCRYPT ’89提出的，其最初用于定义会话密钥交换协议的一种安全性。通俗点解释，就是如果当前会话的密钥协商私钥被破解，只能影响当前会话，不能影响之前历史会话。

对于 RSA 密钥协商来说，如果服务器维护的的私钥被破解，则之前所有历史会话中的加密密钥都被破解了。当然你也可以说，服务器为每次会话都产出一对用来协商的密钥对，但是这个生成过程往往比较耗费资源。

而 DH 算法及其衍生 ECDH 算法，每次会话的密钥交换都是临时生成的密钥对，完全满足 PFS 的要求，且其生成过程相对于 RSA 算法要廉价的多。

综上，我们更倾向于使用 ECDH+AES 的算法组合。

具体选择时，我们可以考虑

  • 对称加密我们可以使用 AES-128 或者 XXTea 算法。
  • 密钥交换使用ECDH算法。

中间人攻击

中间人攻击（英语：Man-in-the-middle attack，简称MITM）是指攻击者与通讯的两端分别创建独立的联系，并交换其所收到的数据，使通讯的两端认为他们正在通过一个私密的连接与对方直接对话，但事实上整个会话都被攻击者完全控制。在中间人攻击中，攻击者可以拦截通讯双方的通话并插入新的内容。在许多情况下这是很简单的（例如，在一个未加密的Wi-Fi的接受范围内的中间人攻击者，可以将自己作为一个中间人插入这个网络）。

一个中间人攻击能成功的前提条件是攻击者能将自己伪装成每一个参与会话的终端，并且不被其他终端识破。中间人攻击是一个（缺乏）相互认证的攻击。其大致过程如下图所示

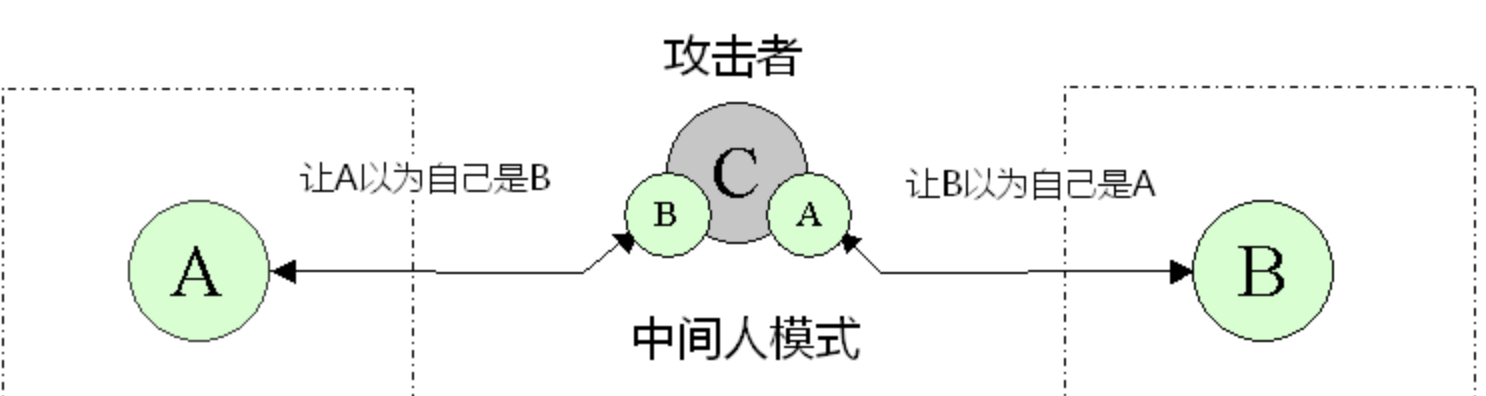
image-20180805200133630

目前，单纯的 ECDH + AES 算法是无法防止中间人攻击的，为此就需要引入身份认证机制，其中使用最多的就是数字认证机制，也就是 CA 证书，这也是目前广泛使用的 Https 协议（本质上是基于 TLS 加密协议）使用的方式。

所谓 CA，即Certificate Authority，就是颁发数字证书的权威机构，充当『公证人』的角色。服务器拿到 CA 颁发的证书，就认为是可以被客户端信赖的，客户端确认了服务器的有效身份，后续的密钥协商和加密通信就可以认为是安全的。

目前常用的数字签名算法有 DSA，RSA，ECDSA(基于 ECC 的 DSA)，其大致原理就是服务器使用私钥对一段信息进行签名(加密)，然后客户端拿到签名时候，使用公钥进行验证(解密)，如果通过，就认为签名有效。

大致原理如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
第1步
服务器方面首先要花一笔银子，在某个 CA 那里购买一个数字证书。
该证书通常会对应几个文件：其中一个文件包含公钥，还有一个文件包含私钥。必须在服务器上部署这两个文件。

第2步
当客户端访问时，服务器首先把包含公钥的证书发送给它。

第3步
客户端验证服务器发过来的证书。如果发现其中有诈，则退出。
由于有了这一步，就大大降低了“中间人攻击”的风险。

为啥客户端（典型的如 https 协议一方的浏览器）能发现 CA 证书是否有诈？
因为正经的 CA 证书，都是来自某个权威的 CA。如果某个 CA 足够权威，那么主流的操作系统（或浏览器）会内置该 CA 的“根证书”。（比如 Windows 中就内置了几十个权威 CA 的根证书）
因此，客户端就可以利用系统内置的根证书，来判断服务器发过来的 CA 证书是不是某个 CA 颁发的。

第4步
如果服务器的 CA 证书没有问题，那么客户端就从该 CA 证书中提取出“公钥”。
然后浏览器随机生成一个“对称加密的密钥”（以下称为 k）。用 CA 证书的公钥加密 k，得到密文 k'，然后把 k' 发送给服务器。

第5步
服务器收到客户端发过来的 k'，用之前保存的私钥进行解密，得到 k。
至此，客户端和服务器都拥有 k，“密钥交换”大功告成啦。

目前来说，数字签名算法+密钥协商算法+对称加密算法的组合相对来说是一种比较安全的加密通信方式，再加上 HMAC 进行摘要完整性校验，可以说能应付大部分普通攻击了。
而通常游戏中返回给客户端进行交互的服务器地址一般是可信赖的服务器 ip 列表，因此目前来说没有使用数字证书来防止中间人攻击的必要。因此此前提到的『密钥协商算法+对称加密算法』组合在游戏通信中得到了普遍应用。

参考资料

密钥交换（密钥协商）算法及其原理

图解SSL/TLS协议